题目
在知乎上偶尔看到一道初中数学题目,所以觉得非常有意思,专门拿出来讨论下。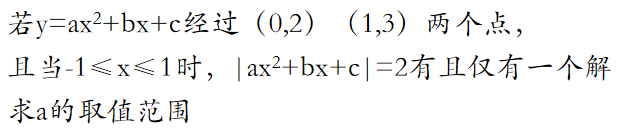
解题思路
分类讨论如下:
- 根据函数经过
(0,2),(1,3)两个点,代入以后可以得到如下等式:
$$
c = 2 \
a + b = 1 \
$$
因此上述函数可以转换为$y = ax^{2} + (1-a)x+2$ - 当且仅当$-1\le x \le 1$时,$|ax^{2} + (1-a)x+2| = 2$仅只有一个解,根据题目中的条件我们知道$|ax^{2} + (1-a)x+2| = 2$目前已经的根为$x=0$,因此我们可以知道以下等式:
$$
|ax^{2} + (1-a)x+2| = 2
$$
在$-1\le x \le 1$有且仅有$x=0$这一个根,要么等式存在其他的根,且其它的根应当满足$x\le -1 , x \ge 1$;要么等式不存在其他的根。我们分情况来讨论,我们首先将上述等式的绝对值拆开,分解为:
$$
ax^{2} + (1-a)x = 0 \qquad (1) \
ax^{2} + (1-a)x + 4 = 0 \qquad (2)
$$
- 首先判断当$a = 0$时,上述两个方程均为一次方程,显然只有
(1)式存在一个根为$x = 0$ - 当$a \neq 0$ 时,上述等式
1与等式2都可能存在两个根。 - 等式
(1)一定存在两个根,分别为$x_{1} = 0,x_{2} = \frac{a-1}{a}$,要们$x_{2} = 0$,要么$x_{2} > 1 ,x_{2} < -1$.
- 等式
- 等式
(2)要么不存在实数的根,要么两个根分布如下:
$$
x_{1} < -1 , x_{2} > 1 \
x_{1} > 1 , x_{2} > 1 \
x_{1} < -1 , x_{2} < -1\
$$
- 等式
- 我们将$a$分开来讨论:
- 当$a = 0$,式
(1)存在根为$x=0$,式(2)不存在根,符合题目要求; - 当$a > 0$时:
- 当$a = 1$时,显然式
1的两个根都为0,式2不存在根,所以符合题目要求。
- 当$a = 1$时,显然式
- 当$a\neq 1$,首先可以判定$\frac{a-1}{a} < 1$,则此时只能满足$\frac{a-1}{a} < -1$,求出此时
a的范围为$0 < a < \frac{1}{2}$.
将上述的$a$的范围.$0< a < \frac{1}{2}$代入到式(2)中发现无解,符合题目要求,即式(1)仅有一个解在$-1\le x \le 1$,且式(2)无解。此时当$a \in (0,\frac{1}{2})$符合题目要求。
- 当$a\neq 1$,首先可以判定$\frac{a-1}{a} < 1$,则此时只能满足$\frac{a-1}{a} < -1$,求出此时
- 当$a < 0$时:
- 当$a < 0$,首先可以判定$\frac{a-1}{a} > 1$一定成立。则此时我们就需要考虑式
2的两个根的情况,我们可以知道式2的根判别式为:
$$
(1-a)^{2} - 16a > a
$$
则当$a < 0$,此时一定存在两个实根分别为,且满足:
$$
x_{1} = \frac{a-1+\sqrt{(a-1)^{2}-16a}}{2a} \
x_{2} = \frac{a-1-\sqrt{(a-1)^{2}-16a}}{2a} \
x_{1} < 0 < x_{2} \
$$
则此时,我们需要判定以下三种情况分别成立时,a的取值范围:
$$
x_{1} < x_{2} < -1 \qquad (a)\
1 < x_{1} < x_{2} \qquad (b)\
x_{1} < -1 , x_{2} > 1 \qquad (c)\
$$
根据简要的判别我们可以知道$(a),(b)$均不可能成立,因此只有$(c)$可能成立,我们求出不等式$c$中a的取值范围如下:
$$
\frac{-3}{2} < a < 0
$$
- 当$a < 0$,首先可以判定$\frac{a-1}{a} > 1$一定成立。则此时我们就需要考虑式
- 综上可知,$a$的取值范围为:
$$
a \in (\frac{-3}{2},\frac{1}{2})\cup{1}
$$
扫描二维码,分享此文章
