leetcode biweekly contest 91
本周的双周赛题目确实不太难,最后一题的二分法确实存在问题,需要举例说明即可。
6237. 不同的平均值数目
给你一个下标从 0 开始长度为 偶数 的整数数组 nums 。
只要 nums 不是 空数组,你就重复执行以下步骤:
- 找到
nums中的最小值,并删除它。 - 找到
nums中的最大值,并删除它。 - 计算删除两数的平均值。
两数 a 和 b 的 平均值 为 (a + b) / 2 。
- 比方说,
2和3的平均值是(2 + 3) / 2 = 2.5。
返回上述过程能得到的 不同 平均值的数目。
注意 ,如果最小值或者最大值有重复元素,可以删除任意一个。
示例 1:
输入:nums = [4,1,4,0,3,5] |
示例 2:
输入:nums = [1,100] |
提示:
2 <= nums.length <= 100nums.length是偶数。0 <= nums[i] <= 100
地址
https://leetcode.cn/contest/biweekly-contest-91/problems/number-of-distinct-averages/
题意
双指针
思路
- 每次取出当前数组中的最大值与最小值,并求二者的平均数,最后用哈希表统计不同数目即可。我们可以先将数组排序 $l$ 指向当前数组的最小值, $r$ 指向当前数组的最大值,每次求完后对索引进行移动即可。
- 复杂度分析:
- 时间复杂度:$O(n \log n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(\log n)$。
代码
class Solution { |
6238. 统计构造好字符串的方案数
给你整数 zero ,one ,low 和 high ,我们从空字符串开始构造一个字符串,每一步执行下面操作中的一种:
- 将
'0'在字符串末尾添加zero次。 - 将
'1'在字符串末尾添加one次。
以上操作可以执行任意次。
如果通过以上过程得到一个 长度 在 low 和 high 之间(包含上下边界)的字符串,那么这个字符串我们称为 好 字符串。
请你返回满足以上要求的 不同 好字符串数目。由于答案可能很大,请将结果对 109 + 7 取余 后返回。
示例 1:
输入:low = 3, high = 3, zero = 1, one = 1 |
示例 2:
输入:low = 2, high = 3, zero = 1, one = 2 |
提示:
1 <= low <= high <= 1051 <= zero, one <= low
地址
https://leetcode.cn/contest/biweekly-contest-91/problems/count-ways-to-build-good-strings/
题意
动态规划
思路
- 非常简单的动态规划,类似于青蛙跳格子或者上楼梯类似的动态规划,在这里对于第 $i$ 个格子有两种路径可以选择要么选择 $zero$,要么选择 $one$。
$$
dp[i] = dp[i - one] + dp[i - zero]
$$ - 复杂度分析:
- 时间复杂度:时间复杂度为 $O(n)$。
- 空间复杂度:空间复杂度为 $O(n)$。
代码
class Solution { |
6240. 树上最大得分和路径
一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
一开始,Alice 在节点
0处,Bob 在节点bob处。每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。对于他们之间路径上的
每一个
节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
示例 1:
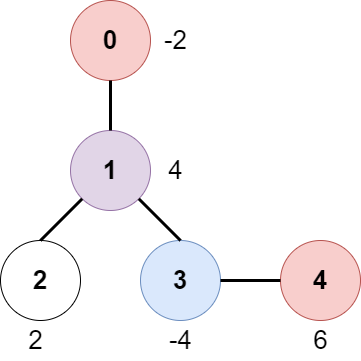
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6] |
示例 2:

输入:edges = [[0,1]], bob = 1, amount = [-7280,2350] |
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-104, 104]之间的一个 偶数 。
地址
https://leetcode.cn/contest/biweekly-contest-91/problems/most-profitable-path-in-a-tree/
题意
深度优先搜索
思路
- 典型的深度优先搜索,但是题目比较长需要仔细阅读题目:
alice从 $0$ 可以到达任意一个叶子节点,即度为 $1$ 的节点。bob从 $bob$ 可以到达 $0$ 节点;alice如果到达的节点bob已经走过的节点,则得分值不一样。
- 从题目中我们可以得知 $bob$ 的路径一定是确定的,且可以知道 $bob$ 途径某个节点 $x$ 的时间为 $time[x]$,因此我们从 $0$ 节点开始依次深度优先搜索到达每个叶子节点,并依次检测路径上的的得分值,找到最小的分值即可。
- 我们依次为路径上的每个节点设定一个时间为 $step[p]$:
- 如果满足 $step[p] > time[p]$,则表示到达当前节点时 $p$ 已经被
bob访问过; - 如果满足 $step[p] < time[p]$,则表示到达当前节点时 $p$ 未被
bob访问过; - 如果满足 $step[p] = time[p]$,则表示到达当前节点时 $p$ 同时被
bob访问;
我们依次找到所有的得分值即可。
- 复杂度分析
- 时间复杂度:时间复杂度为 $O(n)$,$n$ 为给定的节点的数目。仅需两个 $DFS$ 即可。
- 空间复杂度:空间复杂度为 $O(n)$,$n$ 为给定的节点的数目。
代码
class Solution { |
6239. 根据限制分割消息
给你一个字符串 message 和一个正整数 limit 。
你需要根据 limit 将 message 分割 成一个或多个 部分 。每个部分的结尾都是 "<a/b>" ,其中 "b" 用分割出来的总数 替换, "a" 用当前部分所在的编号 替换 ,编号从 1 到 b 依次编号。除此以外,除了最后一部分长度 小于等于 limit 以外,其他每一部分(包括结尾部分)的长度都应该 等于 limit 。
你需要确保分割后的结果数组,删掉每部分的结尾并 按顺序 连起来后,能够得到 message 。同时,结果数组越短越好。
请你返回 message 分割后得到的结果数组。如果无法按要求分割 message ,返回一个空数组。
示例 1:
输入:message = "this is really a very awesome message", limit = 9 |
示例 2:
输入:message = "short message", limit = 15 |
提示:
1 <= message.length <= 104message只包含小写英文字母和' '。1 <= limit <= 104
地址
https://leetcode.cn/problems/height-of-binary-tree-after-subtree-removal-queries/
题意
数学 + 模拟
思路
- 首先我们假设最少可以切分为 $m$ 块,则可以知道第 $i$ 个部分切分的后缀为 $\text{``<i/m>’’}$,第 $i$ 个部分后缀长度为 $|dec(i)| + |dec(m)| + 3$,其中 $dec(i)$ 表示 $i$ 的十进制的位数。我们知道如下信息:
- $|dec(m)|$ 的长度是固定的;
- $|dec(i)|$ 的长度取决于 $i$ 的位数,我们很容易算出。
- 我们很容易通过数学技巧的手段找到小于等于 $m$ 的数中的 $1,2,3,\cdots$ 位数的个数分别为 $f(1),f(2),f(3),\cdots$,可以在 $O(\log_{10}^{n})$ 的时间复杂度内找到上述数的个数。
- 所有后缀的数目之和为 $\sum\limits_{i=1}^{m}(|dec(i)| + |dec(m)| + 3)$,只需要满足 $\sum\limits_{i=1}^{m}(|dec(i)| + |dec(m)| + 3) + n \le limit \times m$,则一定满足填充关系。
综上我们依次从小到大尝试 $m$ 的数目即可,找到符合要求的数目即可。
- 首先这个题目使用二分法存在问题,我们只需找到反例即可,假设当 $m = 99$ 时我们可以满足上述关系,则当 $m = 100$ 时则上述不等式不一定成立,我们可以尝试如下:
如果 $m = 99$ 此时所有的后缀长度为 $\sum\limits_{i=1}^{99}(|dec(i)| + |dec(99)| + 3) = 99 \times 5 + 9 + 90 \times 2 = 684$;
如果 $m = 100$ 此时所有的后缀长度为 $\sum\limits_{i=1}^{100}(|dec(i)| + |dec(99)| + 3) = 100 \times 6 + 9 + 90 \times 2 + 3 = 792$;
我们可以看到实际只增加了后面一个分组但是后缀的总长度增加大概超过了 $100$,我们假设如下不等式成立:
$$
\begin{align*}
\begin{split}
\left {
\begin{array}{lr}
684 + n \le limit \times 99 & \
792 + n > limit \times 100 &
\end{array}
\right.
\end{split}
\end{align*}
$$
我们对上述不等式求解,当 $limit + 684 < 792$ 时上述不等式成立,我们可以取 $limit < 108$ 时,上述不等式成立。因此我们可以观察到并不是随着 $m$ 等增大,成立条件并不满足单调性关系,即如果 $m$ 成立满足条件,则 $m + 1$ 一定也成立满足条件。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示给定的节点的数目。
- 空间复杂度:$O(n)$,其中 $n$ 表示给定的节点的数目。
代码
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://mikemeng.org/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
