kickstart 2021 roundC

最喜欢的kcick start来了，但是由于本次round的时候家里有事，正在陪小孩一直也没有时间来参加，所以只能等到比赛结束后来补上了，非常喜欢google kickstart的题目，质量很高又非常有趣。

a.Smaller Strings (6pts, 9pts)

题目

地址

https://codingcompetitions.withgoogle.com/kickstart/round/0000000000435c44/00000000007ebe5e

题意

数位dp

思路

题目中要求给定的字符串s，长度为n，给定最大字符k,求所出长度为n的且字典序严格小于s的回文字符串的个数，且构成的回文子符串中所有的字符均小于等于k。
典型的数位dp.由于是回文字符串，因此我们只需要找到字符串的前半部分即可，因为后半部分与前半部分相同，我们设dp[i]表示字符串长度为i且符合最大字符小于等于k，且字典序严格小于字符串s的前i个字符构成的字符串的个数。limit表示当前字符串s中的前i个字符是否存在字符大于等于k，limit = 1表示不存在不符合要求的字符，limit = 0表示存在大于k的字符。
我们可以知道递推公式：
当我们选择第i个字符时：

如果当前字符串的前i-1个字符构成的字符串的字典序严格小于s的前i-1个字符构成的字典序，则在第i个字符我们可以在[a,a+k]中我们可以任意取值;
如果当前字符串的前i-1个字符构成的字符串刚好等于s的前i-1个字符构成的字符串，则第i位我们就只能取严格小于s[i]且小于等于“a"+k的字符;

最后需要检测一下，如果把整个数组的前半部分全部转换为回文字符串，则此时需要去检查是否字典序严格小于字符串$s$,算法时间复杂度为$O(n)$.

代码

#include<iostream>
#include<vector>
#include<set>
#include<unordered_set>
#include<map>
#include<unordered_map>
#include<string>
#include<stack>
#include<algorithm>
#include<limits.h>

using namespace std;

void slove(int t){
    int n,k;
    long long ans = 0;
    long long mod = 1e9 + 7;
    string s;
    cin>>n>>k;
    cin>>s;

    /*dp*/
    int m = (n+1)/2;
    int limit = 1;
    vector<long long> dp(m);
    dp[0] = min(s[0]-'a',k);
    for(int i = 1; i < m; ++i){
        if(s[i] -'a' + 1 > k){
            dp[i] = (dp[i-1]*k + k)%mod;
            limit = 0;
        }else{
            dp[i] = (dp[i-1]*k + limit*(s[i]-'a'))%mod;
        }
    }
    ans = dp[m-1];
    if(limit){
        string p = s;
        for(int i = 0; i < m; ++i){
            p[n-1-i] = p[i] = s[i];
        }
        if(p < s) ans = (ans + 1)%mod;
    }
    ans = ans%mod;
    cout<<"Case #"<<t<<": ";
    cout<<ans;
    cout<<endl;
}

int main(){
    int t;
    cin>>t;
    for(int i = 0; i < t; ++i){
        slove(i+1);
    }
    return 0;
}

b. Alien Generato

题目

地址

https://codingcompetitions.withgoogle.com/kickstart/round/0000000000435c44/00000000007ec1cb

题意

数学计算

思路

这个题目非常简单，感觉就是送分题，也就leetcode中等难度的题目。
我们得出计算公式为:
$$
g = n*k + \frac{(n-1)*n}{2} \
k = \frac{g-\frac{(n-1)*n}{2}}{n}
$$
此时我们只需要判断$g-\frac{(n-1)*n}{2}$是否能够整除$n$即可，且商大于等于1.
我们很轻易的可以判断$n \le \sqrt{g}$,我们只需要暴力测试所有可能的n即可。算法时间复杂度为$O(lgn)$.

代码

#include<iostream>
#include<vector>
#include<set>
#include<unordered_set>
#include<map>
#include<unordered_map>
#include<string>
#include<stack>
#include<algorithm>
#include<limits.h>
#include<math.h>

using namespace std;
void slove(int t){
    long long ans = 0;
    long long g;

    cin>>g;
    long long curr = sqrt(g)*2;
    for(long long i = 1; i <= curr; ++i){
        long long x = i*(i-1)/2;
        if(x >= g) break;
        if((g-x)%i == 0){
            ans++;
        }
    }
    cout<<"Case #"<<t<<": ";
    cout<<ans;
    cout<<endl;
}

int main(){
    int t;
    cin>>t;
    for(int i = 0; i < t; ++i){
        slove(i+1);
    }
    return 0;
}

c.Rock Paper Scissors

地址

https://codingcompetitions.withgoogle.com/kickstart/round/0000000000435c44/00000000007ec28e

题意

动态规划

思路

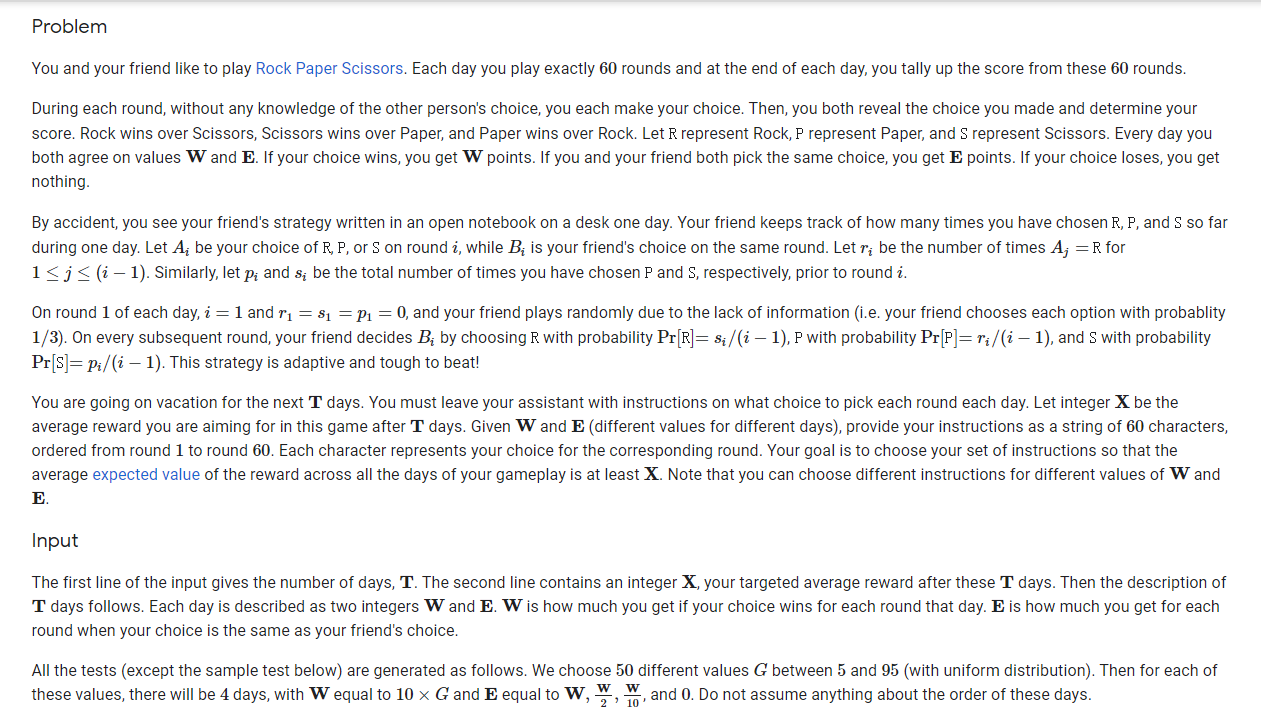
这个题目非常有意思的dp,题目很长，大意就是说两个人玩石头剪刀布的游戏，每个人每轮可以在(r,p,s)分别代表石头、剪刀、布中任意选择一个，石头可以赢剪刀，剪刀可以赢布，布可以赢石头。对方在第i轮出手时，会根据当前已方已经出手的统计次数，来计算出自己选择的概率。假设第i轮时，已方已经出示过的石头、布、剪刀的统计次数分别为$(r_{i},p_{i},s_{i})$,且已知$r_{i} + p_{i} + s_{i} = i$,则在第i+1轮时，对方选择出示石头的概率为$\frac{s_{i}}{i}$，选择布的概率为$\frac{r_{i}}{i}$,选择剪刀的概率为$\frac{p_{i}}{i}$.需要注意的是，在第1轮时，因为没有前面轮次的统计数据，则对方选择出示石头剪刀布的概率均为$\frac{1}{3}$,每天一共需要进行游戏60轮，每天给定每一局赢时获得的分数W，以及平局是获得的分数E，给定一个特定的分数X，求出游戏进行T天后，每天的期望的平均值大于等于X的每天的游戏的出牌方案。
这个题目很长，初看起来还是非常的复杂，不过仔细思考一下，其实也不算是特别难的。首先需要思考的几点:

题目要求给定满足期望平均值大于等于X的方案，那么假设我们每天都以期望最大值即最优的方案来出牌，肯定可以满足题意。所以我们就不用再去讨论其他的可能的方案，按照这个思路转化，本题即转换为求出每天期望值最大的出牌方案。
如果求出期望最大值的方案？实际上应该有多少种组合，我们如果每一轮都按照该轮期望最大值的方案进行出牌是不是一定能够得到最终的期望的最大值？这几个问题是值得深入思考的。
试想如果我们把所有的出牌的顺序的期望值都求一遍，肯定可以求得期望最大值的方案，则此时的算法时间复杂度为$3^{60}$,肯定会超时，有没有可能更简单的枚举方法可以来求？则此时我们应该想到用动态规划的子状态，我们设dp[r][p][s]表示当前已方已经出示了$r$次石头，$p$次布，$s$次剪刀时的最大期望值，则我们可以发现此时游戏一共进行了$ t = r + p + s$轮，则我们发现最优状态与第t轮的选择有直接关系。
我们发现最优状态之间存在关系如下：
- 假设第t轮己方选择的是石头，则第t轮对方选择为剪刀时己方会赢,而此时对方选择为剪刀的概率为$\frac{p}{r+p+s-1}$;对方选择的是石头时，己方会平局，则此时对方选择为石头的概率为$\frac{s}{r+p+s-1}$.因此我们可以推导如下：
  $$
  dp[r][p][s] = max(dp[r][p][s],dp[r-1][p][s] + W\frac{p}{r+p+s-1} + E\frac{s}{r+p+s-1})
  $$
- 假设第t轮己方选择的是布，则第t轮对方选择为石头时己方会赢,而此时对方选择为石头的概率为$\frac{s}{r+p+s-1}$;对方选择的是布时，己方会平局，则此时对方选择为布的概率为$\frac{r}{r+p+s-1}$.因此我们可以推导如下：
  $$
  dp[r][p][s] = max(dp[r][p][s],dp[r][p-1][s] + W\frac{s}{r+p+s-1} + E\frac{r}{r+p+s-1})
  $$
- 假设第t轮己方选择的是剪刀，则第t轮对方选择为布时己方会赢,而此时对方选择为布的概率为$\frac{r}{r+p+s-1}$;对方选择的是剪刀时，己方会平局，则此时对方选择为剪刀的概率为$\frac{p}{r+p+s-1}$.因此我们可以推导如下：
  $$
  dp[r][p][s] = max(dp[r][p][s],dp[r][p][s-1] + W\frac{r}{r+p+s-1} + E\frac{p}{r+p+s-1})
  $$
我们依次遍历所有的可能即可得到在满足$r + p + s = 60$时的最大期望值，并记录下最大期望值时，$(r,p,s)$分别是多少。

最后还有关键的一步，我们如何找到最优的步骤，此时我们可以设定一个数字$choose[r][p][s]$表示当前选择为$(r,p,s)$时，则此时的最后一轮出示的到底是石头、剪刀还是布。我们分别对相应的计数进行减1，寻找前一个最优解的最后一轮出示的内容，则依次我们即可找到最优解，最后进行倒序即可。感觉google给的分析解答貌似表达式有问题，还是自己琢磨最靠谱。

代码

#include<iostream>
#include<vector>
#include<set>
#include<unordered_set>
#include<map>
#include<unordered_map>
#include<string>
#include<stack>
#include<algorithm>
#include<limits.h>
#include<math.h>
#include<cstring>

using namespace std;
void slove(){
    int days,exp_value;
    int win,equal;
    
    cin>>days>>exp_value;
    for(int j = 1; j <= days; ++j){
        string ans;
        cin>>win>>equal;

        //r < p < s < r
        double dp[61][61][61]; 
        char choose[61][61][61];
        memset(dp,0,sizeof(dp));
        memset(choose,0,sizeof(choose));

        /*intial*/
        dp[1][0][0] = double(win + equal)/3;
        choose[1][0][0] = 'R';
        dp[0][1][0] = double(win + equal)/3;
        choose[0][1][0] = 'P';
        dp[0][0][1] = double(win + equal)/3;
        choose[0][0][1] = 'S';
        int x,y,z;
        double maxexpr = 0.0;

        /*get maxmium expect value of each day*/
        for(int i = 2; i <= 60; ++i){
            for(int r = 0; r <= i; ++r){
                for(int p = 0; r + p <= i; ++p){
                    /*all the possible*/
                    int s = i - r - p;
                    double curr = 0.0;
                    // win : (r,s) , euqal (r,r)
                    // we choose "R", friend choose "S" OR "R"
                    if(r > 0){
                        curr = dp[r-1][p][s] + (double)win*(p)/(i-1) + (double)equal*(s)/(i-1);
                        if(curr > dp[r][p][s]){
                            dp[r][p][s] = curr;
                            choose[r][p][s] = 'R';
                        }
                    }
                    // win : (p,r) , euqal (p,p)
                    // we choose "P", friend choose "R" OR "P"
                    if(p > 0) {
                        curr = dp[r][p-1][s] + (double)win*(s)/(i-1) + (double)(equal)*(r)/(i-1);
                        if(curr > dp[r][p][s]){
                            dp[r][p][s] = curr;
                            choose[r][p][s] = 'P';
                        }
                    }     
                    // win : (s,p) , euqal (s,s)
                    // we choose "S", friend choose "P" OR "S"
                    if(s > 0) {
                        curr = dp[r][p][s-1] + (double)win*(r)/(i-1) + (double)(equal)*(p)/(i-1);
                        if(curr > dp[r][p][s]){
                            dp[r][p][s] = curr;
                            choose[r][p][s] = 'S';
                        }
                    }
                    if(i == 60 && dp[r][p][s] > maxexpr){
                        maxexpr = dp[r][p][s];
                        x = r;
                        y = p;
                        z = s;
                    }
                }
            }
        }

        for(int i = 0; i < 60; ++i){
            char c = choose[x][y][z];
            ans.push_back(c);
            if(c == 'R') x--;;
            if(c == 'P') y--;
            if(c == 'S') z--;
        }
        reverse(ans.begin(),ans.end());
        // we just maxium the expect value of dp[60];
        cout<<"Case #"<<j<<": "<<ans<<endl;
    }
}

int main(){
    slove();
}

d.Binary Operator

题目

地址

https://codingcompetitions.withgoogle.com/kickstart/round/0000000000435c44/00000000007ec290

题意

hash

解题思路

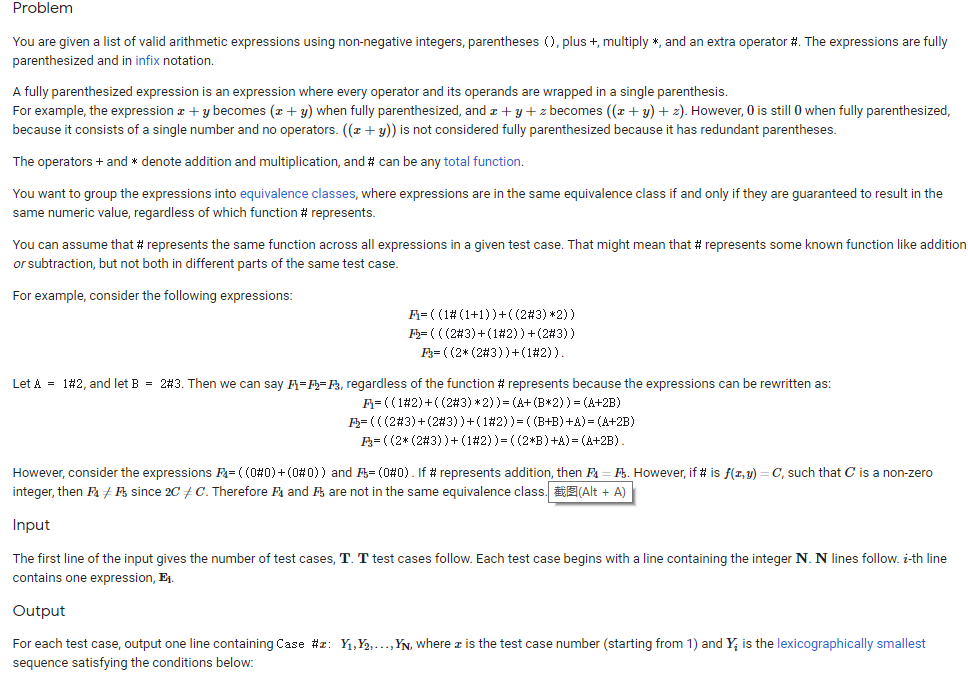
最后一题真心挺难，看了很长时间没有看懂题意,Q4全部做出来且测试用例全部通过的全球不到100人。题目大概的意思是可以对题目中给定的表达式进行化简，然后将化简得表达式进行分类，将表达式相同的进行划分为同一类，最终输出每个表达式的分类。
仔细看一下感觉题目还是非常的复杂，但是最终涉及到需要对表达式进行化简处理，还需要对表达式进行移位和合并计算，刚开始意味非常的麻烦，最后看了大家的解法，各种神奇的解法。

Errichto的解法是用一个非常特殊的hash运算来替代#运算，lucifer1004的解法是把所有可能的运算都计算一遍，如果发现所有可能运算结果都相等，则认为两个表达式相等，否则则认为不相等。确实是暴力出奇迹的解法,如果按照这两种思路来求解表达式的值的话，这题反而没有那么难了，仔细检查了一下答案发现好多人都用这种解法来完成，当然这种解法存在一定的概率导致出现冲突而计算错误，但是实际商概率非常小。

主要是题目中涉及到这个#的处理，如果完全用表达式的话，则确实不太好处理，反而我们换种思路去测试它的计算结果是否一致来检测两个表达式是否相等。求该表达式求值本身比较简单，利用后缀式即可，利用栈来处理，这个是常规做法。
官方给的解答是将所有的表达式转化为逆波兰式，然后再通过某种调整的方法对二叉树进行调整，最终判定逆波兰式的二叉树是否相等，不过确实好复杂。

代码

暴力测试所有可能的运算

from sys import stdin
from random import randint

randoms = [randint(-1000, 1000) for _ in range(100)]


def read_int():
    return int(stdin.readline())


def read_ints():
    return map(int, stdin.readline().split(' '))


def plus(x, y):
    return x + y + randoms[0]


def sub(x, y):
    return x - y + randoms[1]


def mul(x, y):
    return x * y + randoms[2]


def my_div(x, y):
    return x // (abs(y) + 1) + randoms[3]


def my_inv_div(x, y):
    return y // (abs(x) + 1) + randoms[4]


def my_mod(x, y):
    return x % (abs(y) + 1) + randoms[5]


def my_inv_mod(x, y):
    return y % (abs(x) + 1) + randoms[6]


def bit_and(x, y):
    return x & y + randoms[7]


def bit_or(x, y):
    return x | y + randoms[8]


def bit_xor(x, y):
    return x ^ y + randoms[9]


def const(x, y):
    return randoms[10]


def only_x(x, y):
    return x + randoms[11]


def only_y(x, y):
    return y + randoms[12]


def quad_x(x, y):
    return x * x + y + randoms[13]


def quad_y(x, y):
    return x + y * y + randoms[14]


funcs = [plus, sub, mul, my_div, my_mod, my_inv_div, my_inv_mod,
         bit_and, bit_or, bit_xor, const, only_x, only_y, quad_x, quad_y]


class Expression:
    def __init__(self, s):
        self.s = '(' + s + ')'

    def evaluate(self, func):
        nums = []
        ops = []
        curr = 0
        is_num = False
        for c in self.s:
            if c == '(':
                if is_num:
                    nums.append(curr)
                    is_num = False
                ops.append('(')
            elif c in '+*#':
                if is_num:
                    nums.append(curr)
                    is_num = False
                ops.append(c)
            elif c == ')':
                if is_num:
                    nums.append(curr)
                    is_num = False
                while ops[-1] != '(':
                    op = ops.pop()
                    b = nums.pop()
                    a = nums.pop()
                    if op == '+':
                        nums.append(a + b)
                    elif op == '*':
                        nums.append(a * b)
                    else:
                        nums.append(func(a, b))
                ops.pop()
            else:
                if not is_num:
                    curr = 0
                    is_num = True
                curr = curr * 10 + int(c)
        assert(len(nums) == 1)
        return nums[0]

    def __eq__(self, other):
        for func in funcs:
            a = self.evaluate(func)
            b = other.evaluate(func)
            if a != b:
                return False
        return True


t = read_int()
for case_num in range(1, t + 1):
    n = read_int()
    expressions = [Expression(input()) for _ in range(n)]

    color = [0] * n
    color[0] = 1
    new_color = 2
    for i in range(1, n):
        for j in range(i):
            if expressions[i] == expressions[j]:
                color[i] = color[j]
                break
        if color[i] == 0:
            color[i] = new_color
            new_color += 1

    print(f"Case #{case_num}: {' '.join(map(str, color))}")

利用特殊的hash替代#

#include <bits/stdc++.h>
using namespace std;
#define sim template < class c
#define ris return * this
#define dor > debug & operator <<
#define eni(x) sim > typename \
  enable_if<sizeof dud<c>(0) x 1, debug&>::type operator<<(c i) {
sim > struct rge { c b, e; };
sim > rge<c> range(c i, c j) { return rge<c>{i, j}; }
sim > auto dud(c* x) -> decltype(cerr << *x, 0);
sim > char dud(...);
struct debug {
#ifdef LOCAL
~debug() { cerr << endl; }
eni(!=) cerr << boolalpha << i; ris; }
eni(==) ris << range(begin(i), end(i)); }
sim, class b dor(pair < b, c > d) {
  ris << "(" << d.first << ", " << d.second << ")";
}
sim dor(rge<c> d) {
  *this << "[";
  for (auto it = d.b; it != d.e; ++it)
	*this << ", " + 2 * (it == d.b) << *it;
  ris << "]";
}
#else
sim dor(const c&) { ris; }
#endif
};
#define imie(...) " [" << #__VA_ARGS__ ": " << (__VA_ARGS__) << "] "
// debug & operator << (debug & dd, P p) { dd << "(" << p.x << ", " << p.y << ")"; return dd; }

const int mod = 1000050131;

char s[10005];

int hasz(int a) {
	return ((100594677LL * (a + 450617412)) ^ 208774486) % mod;
}

int merge(int a, int b, char ope) {
	if(ope == '+') {
		return (a + b) % mod;
	}
	if(ope == '*') {
		return (long long) a * b % mod;
	}
	assert(ope == '#');
	return (((337807718LL * hasz(a)) + 254452523) ^ ((842188890LL * hasz(b)) + 900099649)) % mod;
}

int get_balance(char c) {
	if(c == '(') {
		return 1;
	}
	if(c == ')') {
		return -1;
	}
	return 0;
}

int rec(int L, int R) {
	// debug() << imie(L) imie(R);
	int bal = 0;
	for(int i = L; i <= R; ++i) {
		bal += get_balance(s[i]);
	}
	assert(bal == 0);
	if(s[L] == '(') {
		int balance = 1;
		int i = L + 1;
		while(balance > 0) {
			balance += get_balance(s[i]);
			i++;
		}
		// past closing bracket
		int a = rec(L + 1, i - 2); // this was inside the brackets
		if(i >= R) {
			return a;
		}
		assert(s[i] == '#' || s[i] == '+' || s[i] == '*');
		// debug() << imie(i+1) imie(R);
		int b = rec(i + 1, R);
		return merge(a, b, s[i]);
	}
	int a = 0;
	while(L <= R && isdigit(s[L])) {
		a = (10LL * a + (s[L] - '0')) % mod;
		L++;
	}
	if(L > R) {
		return a;
	}
	// debug() << imie(L);
	assert(s[L] == '+' || s[L] == '*' || s[L] == '#');
	int b = rec(L + 1, R);
	return merge(a, b, s[L]);
}

void test_case() {
	int n;
	scanf("%d", &n);
	map<int, int> mapping;
	for(int i = 0; i < n; ++i) {
		scanf("%s", s);
		int value = rec(0, (int) strlen(s) - 1);
		if(mapping.find(value) == mapping.end()) {
			int nxt = mapping.size();
			nxt++;
			mapping[value] = nxt;
		}
			printf(" %d", mapping[value]);
		// debug() << imie(value);
	}
		puts("");
}

int main() {
	int T;
	scanf("%d", &T);
	for(int z = 1; z <= T; z++) {
		printf("Case #%d:", z);
		test_case();
	}
}

欢迎关注和打赏，感谢支持！

关注我的博客: http://mikemeng.org/
关注我的知乎：https://www.zhihu.com/people/da-hua-niu
关注我的微信公众号: 公务程序猿

Tags: kickstart

← kickstart 2021 round G 【kickstart】 kickstart 2021 roundD →

扫描二维码，分享此文章

【kickstart】 kickstart 2021 roundC

kickstart 2021 roundC

a.Smaller Strings (6pts, 9pts)

题目

地址

题意

思路

代码

b. Alien Generato

题目

地址

题意

思路

代码

c.Rock Paper Scissors

地址

题意

思路

代码

d.Binary Operator

题目

地址

题意

解题思路

代码