天堂硅谷·数字经济算法编程大赛

题目质量还算可以，依旧三题的节奏

题目-01. 化学反应

题目

实验室内有一些化学反应物，其中的任意两种反应物之间都能发生反应，且质量的消耗量为 1:1

已知初始 material[i] 表示第 i 种反应物的质量，每次进行实验时，会选出当前 质量最大 的两种反应物进行反应，假设反应物的重量分别为 i 和 j ，且 i <= j。反应的结果如下：

• 如果 i == j，那么两种化学反应物都将被消耗完；
• 如果 i < j，那么质量为 i 的反应物将会完全消耗，而质量为 j 的反应物质量变为 j - i 。
  最后，最多只会剩下一种反应物，返回此反应物的质量。如果没有反应物剩下，返回 0。

示例 1：

输入：[10,2,6,1]
输出：1
解释：
先选出 10 和 6，得到 4，数组转换为 [4,2,1]，
再选出 4 和 2，得到 2，数组转换为 [2,1]，
最后选出 2 和 1，得到 1，最终数组转换为 [1]，这就是最后剩下反应物的质量。

示例 2：

输入：[6,4,10]
输出：0
解释：
先选出 10 和 6，得到 4，所以数组转换为 [4,4]，
再选出 4 和 4，得到 0，所以数组转换为 []
因为没有反应物剩下，返回 0。

提示：

• 1 <= material.length <= 30
• 1 <= material[i] <= 1000

地址

https://leetcode.cn/problems/6CE719/

题意

堆

思路

1. 典型的堆运算，每次选取序列中质量最大的两个元素，然后将其相减的结果加入到堆中，重复上述操作直到堆中的元素为 $0$ 个或者 $1$ 个则结束。需要注意的是当取出的两个元素相等时，则不会再往堆中放回元素。
2. 复杂度分析：

• 时间复杂度：$O(n \log n)$，其中 $n$ 表示数组的长度。
• 空间复杂度：$O(n)$。

代码

class Solution {
public:
    int lastMaterial(vector<int>& material) {
        priority_queue<int, vector<int>, less<int>> pq;
        for (auto v : material) {
            pq.emplace(v);
        }
        
        while (pq.size() > 1) {
            int x = pq.top();
            pq.pop();
            int y = pq.top();
            pq.pop();
            if (x > y) {
                pq.emplace(x - y);
            }
        }
        if (pq.size() > 0) {
            return pq.top();
        } else {
            return 0;
        }
    }
};

题目-02. 销售出色区间

题目

给你一份销售数量表 sales，上面记录着某一位销售员每天成功推销的产品数目。

我们认为当销售员同一天推销的产品数目大于 8 个的时候，那么这一天就是「成功销售的一天」。

所谓「销售出色区间」，意味在这段时间内，「成功销售的天数」是严格 大于「未成功销售的天数」。

请你返回「销售出色区间」的最大长度。

示例 1：

输入：sales = [10,2,1,4,3,9,6,9,9]
输出：5
解释：最大销售出色区间是 [3,9,6,9,9]。

示例 2：

输入：sales = [5,6,7]
输出：0

提示：

• 1 <= sales.length <= 104
• 0 <= sales[i] <= 16

地址

https://leetcode.cn/contest/hhrc2022/problems/0Wx4Pc/

题意

前缀和 + 贪心法则

思路

1. 我们当前元素如果 $\textit{sales}[i] > 8$ 则记为 $1$，否则记为 $-1$，并用数组 $\textit{arr}$ 进行记录，然后我们统计 $arr$ 的前缀和，此时我们知道：

• 如果 $sum[i] > 0$ 则表示数组前 $i$ 项中正数的数目大于负数的数目，则该区间为销售出色区间。则此时以 $i$ 为终点的最大销售出色区间长度为 $i$。
• 如果 $sum[i] \le 0$ 则表示数组前 $i$ 项中正数的数目小于等于负数的数目，则该区间不为销售出色区间。此时我们知道以 $i$ 为终点的最大区间则为 $sum[i] - cnt[sum[i] - 1]$

2. 复杂度分析：

• 时间复杂度：时间复杂度为 $O(n)$，其中 $n$ 表示节点的数目。
• 空间复杂度：空间复杂度为 $O(n)$，其中 $n$ 表示节点的数目。

代码

class Solution {
public:
    int longestESR(vector<int>& sales) {
        int n = sales.size();
        unordered_map<int, int> cnt;
        int prevSum = 0;
        int res = 0;
        for (int i = 0; i < n; i++) {
            prevSum += (sales[i] > 8 ? 1 : -1); 
            if (prevSum > 0) {
                res = max(res, i + 1);
            } 
            if (cnt.count(prevSum - 1)) {
                res = max(res, i - cnt[prevSum - 1]);
            }
            if (!cnt.count(prevSum)) {
                cnt[prevSum] = i;
            }
        }
        return res;
    }
};

题目-03. 重复的彩灯树

题目

有一棵结构为二叉树的圣诞树 root 挂满了彩灯，各节点值表示彩灯的颜色。

如果两棵子树具有 相同的结构 和 相同的彩灯颜色分布，则它们是 重复 的。

请返回这棵树上所有 重复的子树。

注意：

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

示例 1：

输入：root = [1,3,3,null,2,null,2]
输出：[[3,null,2],[2]]

示例 2：

输入：root = [3,3,2,null,2]
输出：[[2]]

示例 3：

输入：root = [1,3,3,null,2,2]
输出：[[2]]

提示：

• 树中的结点数在 [1,6000] 范围内。
• -200 <= Node.val <= 200

地址

https://leetcode.cn/problems/EXvqDp/

题意

模拟

思路

1. 我们直接将子树转换为字符串即可，具体子树转换为字符串的方式有许多中，可以参考力扣上的关于二叉树转换为字符串的题目，所以非常简单的题目了。
2. 复杂度分析

• 时间复杂度：时间复杂度为 $O(n^2)$，$n$ 为节点的数目。
• 空间复杂度：时间复杂度为 $O(n^2)$，$n$ 为节点的数目。

代码

class Solution {
public:
    string dfs(TreeNode* root, unordered_map<string, vector<TreeNode *>> &cnt) {
        if (!root) {
            return "null";
        }
        string left = dfs(root->left, cnt);
        string right = dfs(root->right, cnt);
        string str =  "(" + left + ")" + to_string(root->val) + "(" + right + ")";
        cnt[str].emplace_back(root);
        return str;
    }
    
    vector<TreeNode*> lightDistribution(TreeNode* root) {
        unordered_map<string, vector<TreeNode *>> cnt;
        dfs(root, cnt);
        vector<TreeNode *> res;
        for (auto [_, vec] : cnt) {
            if (vec.size() > 1) {
                res.emplace_back(vec[0]);
            }
        }
        return res;
    }
};

题目-04. 补给覆盖

题目

已知有一片呈二叉树的道路，我们要在道路上的一些节点设置补给站支援。

补给站可以设置在任意节点上，每个补给站可以使距离自身小于等于 1 个单位的节点获得补给。

若要使道路的所有节点均能获得补给，请返回所需设置的补给站最少数量。

示例 1：

输入：[0,0,0]
输出：1
解释：如图所示，一个补给站足够使道路的所有节点获得补给。

示例 2：

输入：[0,0,0,null,null,null,0]
输出：2
解释：需要至少设置两个补给站来使道路的所有节点获得补给。 上图显示了补给站设置的有效位置之一。

提示：

• 节点的数量范围为 [1, 1000]。
• 每个节点的值均为 0 。

地址

https://leetcode.cn/contest/weekly-contest-312/problems/number-of-good-paths/

题意

动态规划

思路

1. 设 $dp[node][0], dp[node][1], dp[node][2]$ 分别表示节点 $node$ 构成的子树全部可以获得补给的最小数量：

• $dp[node][0]$ 表示 $node$ 会被父节点补给的最少数量；
• $dp[node][1]$ 表示 $node$ 会被其孩子节点补给的最少数量；
• $dp[node][2]$ 表示 $node$ 会被自身补给的最少数量；

则我们可以知道有以下推论：

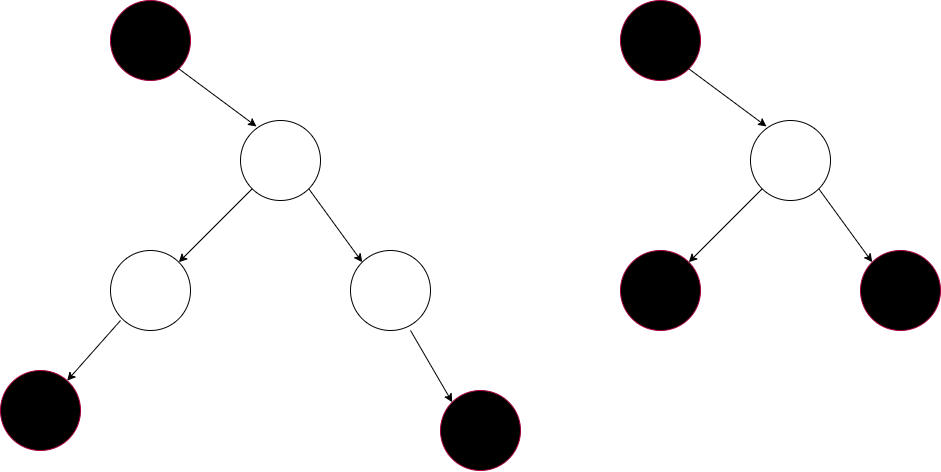
• 如果 $node$ 会被父节点补给，则此时 $node$ 的子节点此时要么被自身补给，要么被 $node$ 的子节点的子节点补给，且此时 $node$ 子节点不能被 $node$ 补给；所以可以得到以下推论:
  $$
  dp[node][0] = \min(dp[node.left][1],dp[node.left][2]) + \min(dp[node.right][1],dp[node.right][2])
  $$
  

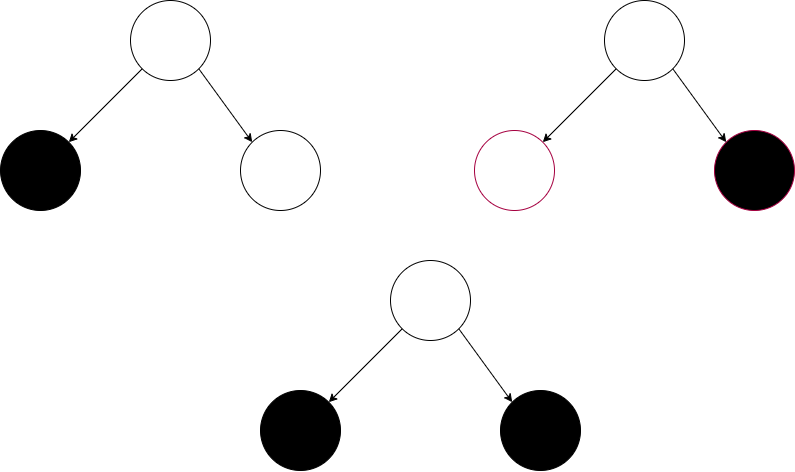
• 如果 $node$ 会被孩子节点补给，则此时 $node$ 的子节点中一定有一个子节点被自身补给，$node$ 的左孩子要么为补给站要么右孩子为补给站，即两个孩子节点中至少有一个为补给站，所以可以得到以下推论:
  $$
  dp[node][1] = \min((dp[node.left][1] + \min(dp[node.right][1], dp[node.right][2]), (dp[node.right][1] + \min(dp[node.left][1], dp[node.left][2]))
  $$
  

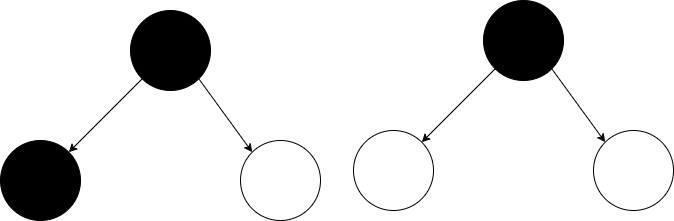
• 如果 $node$ 会被自身补给，则此时 $node$ 的子节点可以被 $node$ 补给或者被自身、孩子节点补给，此时需要在 $node$ 处放置一个补给站，所以可以得到以下推论:
  $$
  dp[node][2] = 1 + \min(dp[node.left][0],dp[node.left][1], dp[node.left][2]) + \min(dp[node.left][0],dp[node.left][1], dp[node.left][2])
  $$
  

2. 复杂度分析：

• 时间复杂度：$O(m \log m + n \times \alpha(n))$，其中 $m$ 表示边的数目，$n$ 表示节点的数目。
• 空间复杂度：$O(n)$，$n$ 表示节点的数目。

代码

class Solution {
public:
    /* [a, b, c], a : chose by father, b : chose by child, c : chose by self */
    int minSupplyStationNumber(TreeNode* root) {
        function<tuple<int,int,int>(TreeNode *)> dfs = [&](TreeNode* root)->tuple<int,int,int> {
            if (root == nullptr) {
                return {0, 0, 1};
            }
            auto [la, lb, lc] = dfs(root->left);
            auto [ra, rb, rc] = dfs(root->right);
            int a = min(lb, lc) + min(rb, rc);
            int b = min(lc + min(rb, rc), rc + min(lb, lc));
            int c = 1 + min({la, lb, lc}) + min({ra, rb, rc});
            return {a, b, c};
        };
        auto [a, b, c] = dfs(root);
        return min(b, c);
    }
};

欢迎关注和打赏，感谢支持！

• 关注我的博客: http://mikemeng.org/
• 关注我的知乎：https://www.zhihu.com/people/da-hua-niu
• 关注我的微信公众号: 公务程序猿