leetcode biweekly contest 86
最后一题翻译太稀烂,错了好长时间,最后只能看英文。
6171. 和相等的子数组
题目
给你一个下标从 0 开始的整数数组 nums ,判断是否存在 两个 长度为 2 的子数组且它们的 和 相等。注意,这两个子数组起始位置的下标必须 不相同 。
如果这样的子数组存在,请返回 true,否则返回 false 。
子数组 是一个数组中一段连续非空的元素组成的序列。
示例 1:
输入:nums = [4,2,4] |
示例 2:
输入:nums = [1,2,3,4,5] |
示例 3:
输入:nums = [0,0,0] |
提示:
2 <= nums.length <= 1000-109 <= nums[i] <= 109
`
地址
https://leetcode.cn/contest/biweekly-contest-86/problems/find-subarrays-with-equal-sum/
题意
哈希统计
思路
- 简单题目,我们直接统计所有相邻两个元素的和,如果出现相同,则返回 $true$,否则则返回 $false$.
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
代码
class Solution { |
6172. 严格回文的数字
题目
如果一个整数 n 在 b 进制下(b 为 2 到 n - 2 之间的所有整数)对应的字符串 全部 都是 回文的 ,那么我们称这个数 n 是 严格回文 的。
给你一个整数 n ,如果 n 是 严格回文 的,请返回 true ,否则返回 false 。
如果一个字符串从前往后读和从后往前读完全相同,那么这个字符串是 回文的 。
示例 1:
输入:n = 9 |
示例 2:
输入:n = 4 |
提示:
4 <= n <= 105
地址
https://leetcode.cn/contest/biweekly-contest-86/problems/strictly-palindromic-number/
题意
直接检测
思路
- 这个就非常直接了,直接将 $n$ 分别转换为对应 $[2,n-2]$ 进制数,然后依次检测转换后的数 $x$ 是否时回文即可。
- 复杂度分析:
- 时间复杂度:时间复杂度为 $O(n \log n)$,$n$ 表示给定的元素 $n$。
- 空间复杂度:时间复杂度为 $O(\log n)$,$n$ 表示给定的元素 $n$。
代码
class Solution { |
6173. 被列覆盖的最多行数
题目
给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ,表示你需要选出的列数。
如果一行中,所有的 1 都被你选中的列所覆盖,那么我们称这一行 被覆盖 了。
请你返回在选择 cols 列的情况下,被覆盖 的行数 最大 为多少。
示例 1:
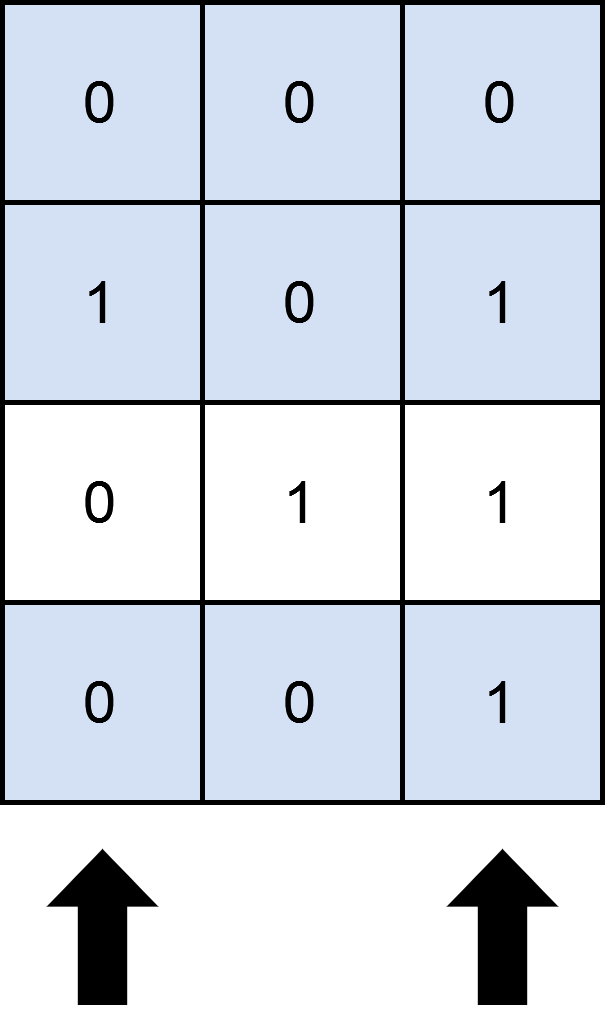
输入:mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2 |
示例 2:

输入:mat = [[1],[0]], cols = 1 |
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 12mat[i][j]要么是0要么是1。1 <= cols <= n
地址
https://leetcode.cn/contest/biweekly-contest-86/problems/maximum-rows-covered-by-columns/
题意
位图运算
思路
- 我们可以将矩阵中的第 $i$ 行都转换为二进制位图 $mask[i]$;我们依次检测 $i$ 所代表的列的位图,其中 $i$ 的第 $k$ 为 $1$ 则表示将矩阵的第 $k$ 列进行覆盖,我们依次检测每一行是否在位图 $i$ 所代表的覆盖方案下,该行中的 $1$ 是否全部被覆盖,我们可以用位运算,如果满足:
$mask[j] \And i = mask[j]$
则 $mask[j]$ 一定是 $i$ 的子集,此时 $i$ 一定可以覆盖 $mask[j]$,从而我们即可判断出有多少行可以被覆盖。
2. 复杂度分析
- 时间复杂度:时间复杂度为 $O(m \times n + m \times 2^n)$,其中 $m,n$ 分别为矩阵的行数与列数。
- 空间复杂度:空间复杂度为 $O(m)$,其中 $m$ 为矩阵的行数。
代码
class Solution { |
6143. 预算内的最多机器人数目
题目
你有 n 个机器人,给你两个下标从 0 开始的整数数组 chargeTimes 和 runningCosts ,两者长度都为 n 。第 i 个机器人充电时间为 chargeTimes[i] 单位时间,花费 runningCosts[i] 单位时间运行。再给你一个整数 budget 。
运行 k 个机器人 总开销 是 max(chargeTimes) + k * sum(runningCosts) ,其中 max(chargeTimes) 是这 k 个机器人中最大充电时间,sum(runningCosts) 是这 k 个机器人的运行时间之和。
请你返回在 不超过 budget 的前提下,你 最多 可以 连续 运行的机器人数目为多少。
示例 1:
输入:chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25 |
示例 2:
输入:chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19 |
提示:
chargeTimes.length == runningCosts.length == n1 <= n <= 5 * 1041 <= chargeTimes[i], runningCosts[i] <= 1051 <= budget <= 1015
`
地址
https://leetcode.cn/contest/biweekly-contest-86/problems/maximum-number-of-robots-within-budget/
题意
滑动窗口
思路
- 二分查找的解法就比较简单了,时间复杂度为 $n \times (\log n)^2$,在题目给定的测试用例下会超时。
- 我们还可以采用滑动窗口的解法,设当前窗口为 $[j,i]$, 每次我们向右移动一个位置后,此时窗口变为 $[i, j +1]$,我们检测当前的窗口是否满足题目要求,如果满足则记录,否则则将窗口的左起点进行缩小知道窗口满足题目要求即可。需要使用技巧的是,我们可以用 $treeset$ 保存窗口中的所有数据,可以在 $O(1)$ 的时间复杂度内得到窗口中最大的值即可。
- 复杂度分析:
- 时间复杂度:$O(n \times \log n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$(n)$,其中 $n$ 表示数组的长度。
代码
class Solution { |
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://mikemeng.org/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章
