且听疯吟

AutoX 安途智行专场竞赛

2022-11-01

AutoX 安途智行专场竞赛

几场企业的题目质量都还挺高，比周赛题目好多了，今天周赛又是手速场。题目也有意思多了，建议多来点这样的题目。

AutoX-1. 网页瀑布流

题目

网页布局中有一种瀑布流布局方式，表现为参差不齐的多栏布局。随着页面滚动条向下，还会不断加载数据块并附加至当前尾部。页面在加载时遵循以下规则：

  • 当有数据块需要加载时，优先加载在高度最短的那一列；
  • 若存在多个高度相同且最短的情况，则加载在其中最靠左的那一列

已知当前网页共分割为 num 列，该网页有若干数据块可以加载，block[i] 表示第 i 个数据块的高度。当页面按顺序加载完所有的数据块后，请返回高度最大的那一列的高度。

示例 1：

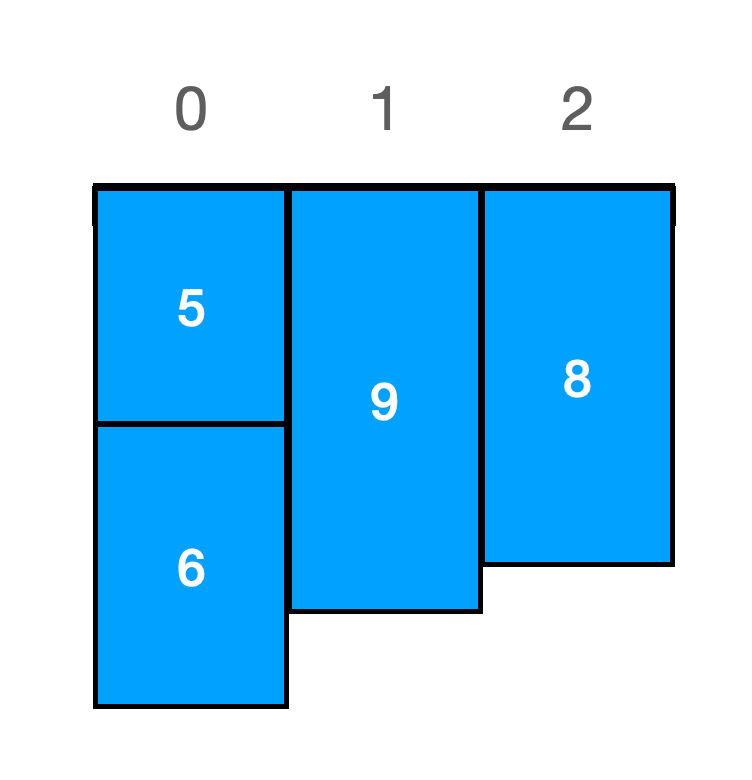
输入：num = 3, block = [5,9,8,6]

输出：11

解释：如下图所示，返回 11
image.png

示例 2：

输入：num = 2, block = [9,1,1,1,1,1]

输出：9

提示：

  • 0 < num <= 100
  • 0 < block.length <= 10^4
  • 0 < block[i] <= 10^3

地址

https://leetcode.cn/contest/autox2023/problems/l9HbCJ/

题意

堆

思路

  1. 可以算是简单题目了，一旦堆中的元素的数目达到 $nums$ 个，则此时我们每次从堆中取出最小元素与当前元素相加之后再放回堆中，让堆中的元素的数目始终保持在 $nums$ 个，最后求出堆中最大的元素即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n \log k)$，其中 $n$ 表示数组的长度, $k$ 为题目指定的大小。
  • 空间复杂度：$O(k)$。$k$ 为题目指定的大小。

代码

class Solution {
public:
    int getLengthOfWaterfallFlow(int num, vector<int>& block) {
        priority_queue<int, vector<int>, greater<int>> pq;
        for (auto v : block) {
            if (pq.size() < num) {
                pq.emplace(v);
            } else {
                int curr = pq.top();
                pq.pop();
                pq.emplace(curr + v);
            }
        }
        int ans = 0;
        while (!pq.empty()) {
            ans = max(ans, pq.top());
            pq.pop();
        }
        return ans;
    }
};

AutoX-2. 蚂蚁王国的蜂蜜

题目

蚂蚁王国的蜂蜜专家旺财最近在研究蜂蜜的价格，为了估算出真实的蜂蜜价格，旺财以所有用有效报价的平均值作为蜂蜜均价，稳定的报价往往方差也比较小。因为情报具有时效性，所以每隔一段时间，旺财也会删除一些老旧报价。
因为计算平均值和方差对于蚂蚁是一个困难的问题，所以旺财希望你帮他设计一个系统，handle[i] = [type] 或 [type, value] 表示对于旺财的第 i 次的操作有：

  • 若 type 为 1，表示获取了一份价格为 value 的报价
  • 若 type 为 2，表示删除了一个价格为 value 的报价
  • 若 type 为 3，表示计算当前蜂蜜的均价；若当前不存在任何有效报价，返回 -1
  • 若 type 为 4，表示计算当前价格的方差；若当前不存在任何有效报价，返回 -1

请按操作的顺序，依次返回所有计算均价和方差的结果。

提示：

  • 用例保证所有删除的报价都是有效的。

示例 1：

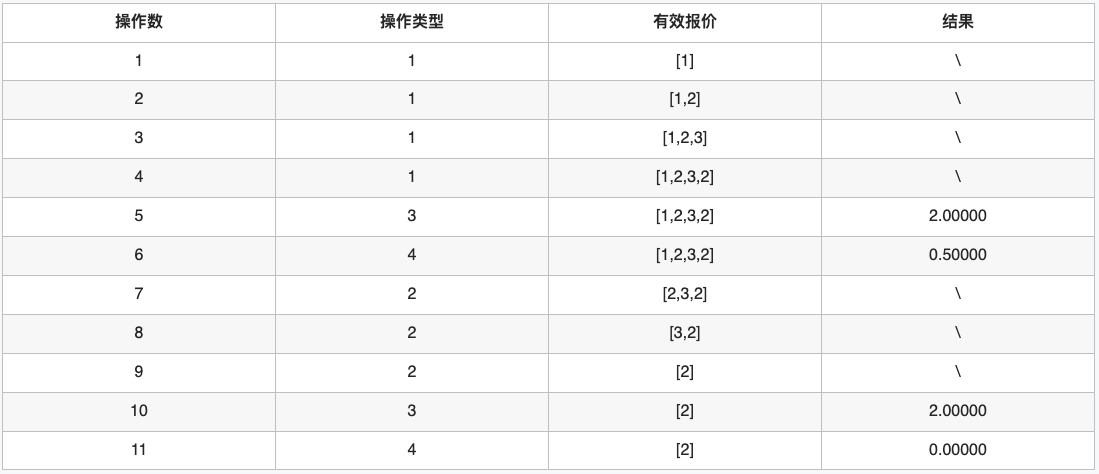
输入：handle = [[1,1],[1,2],[1,3],[1,2],[3],[4],[2,1],[2,2],[2,3],[3],[4]]

输出：[2.00000,0.50000,2.00000,0.00000]

解释：如下表所示
image.png

示例 2：

输入：handle = [[3],[1,10],[1,0],[3],[4],[2,10],[3]]

输出：[-1.00000,5.00000,25.00000,0.00000]

提示：

  • 0 <= handle.length <=10^5
  • 0 <= handle[i][1] <= 100
  • handle[i][0] 仅包含 1,2,3,4

地址

https://leetcode.cn/contest/autox2023/problems/8p6t8R/

题意

数学

思路

  1. 本质是数学问题，求方差和平均值。题目中关键信息为 0 <= handle[i][1] <= 100，我们直接用哈希表统计当前元素的个数即可，意味当前保存的不同元素的种类不会超过 $101$ 个：
  • 平均值：我们保存当前的元素的总和 $sum$ 与总的个数 $total$，每次从价格中删除和添加元素，我们同时更新 $sum$ 和 $total$ 即可，此时均价为 $\dfrac{sum}{total}$。
  • 方差：我们已知平均数为 $\dfrac{sum}{total}$，设此时哈希表中存储的 $k$ 个元素分别为 $p_1, p_2, \cdots, p_k$，元素的个数分别为 $c_1, c_2, \cdots, c_k$，则此时可以知道方差为 $\dfrac{\sum_{i=1}^{k} \limits c_i * (p_i - \frac{sum}{total})^{2}}{total}$。
  1. 复杂度分析：
  • 时间复杂度：时间复杂度为 $O(n \times \max (price))$，$n$ 表示插入元素的个数，$\max (price)$ 表示元素的最大数。
  • 空间复杂度：时间复杂度为 $O(\max (price))$，$\max (price)$ 表示元素的最大数。

代码

class Solution {
public:
    vector<double> honeyQuotes(vector<vector<int>>& handle) {
        unordered_map<int,int> cnt;
        int total = 0;
        int sum = 0;
        vector<double> ret;
        for (auto v : handle) {
            if (v[0] == 1) {
                cnt[v[1]]++;
                total++;
                sum += v[1];
            } else if(v[0] == 2) {
                cnt[v[1]]--;
                if (cnt[v[1]] == 0) {
                    cnt.erase(v[1]);
                }
                total--;
                sum -= v[1];
            } else if(v[0] == 3) {
                if (total == 0) {
                    ret.emplace_back(-1);
                } else {
                    ret.emplace_back((double)sum / total);
                }
            } else if(v[0] == 4) {
                if (total == 0) {
                    ret.emplace_back(-1);
                } else {
                    double avg = (double)sum / total;
                    double variance = 0;
                    for (auto &&[x, freq] : cnt) {
                        variance += ((double)x - avg)*((double)x - avg) * freq;
                    }
                    ret.emplace_back(variance / total);
                }
            }
        }
        return ret;
    }
};

AutoX-3. 出行的最少购票费用

题目

航空公司向经常乘坐飞机的乘客们提供了一些商务套票，tickets[i] = [duration_i, price_i]，表示第 i 种套票的有效天数和价格。

例如：乘客购买了有效天数为 n 的套票，则该套票在第 date ~ date+n-1 天期间都可以使用。

现有一名乘客将在未来的几天中出行，days[i] 表示他第 i 次出行的时间，如果他选择购买商务套票，请返回他将花费的最少金额。

注意：

  • 输入不存在多个有效天数相同的套票。

示例 1：

输入：
days = [1,2,3,4]
tickets = [[1,3],[2,5],[3,7]]

输出: 10

解释：可以买一张一天有效期的票和一张三天有效期的票；或买两张两天有效期的票；总票价均为10

示例 2：

输入：
days = [1,4,5]
tickets = [[1,4],[5,6],[2,5]]

输出: 6

解释：买一张 5 天有效期的票；总票价为6

提示：

  • 1 <= days.length <= 10^5
  • 1 <= days[i] < days[i+1] <= 10^9
  • 1 <= tickets.length <= 20
  • 1 <= tickets[i][0] <= 10^5
  • 1 <= tickets[i][1] <= 10^9

地址

https://leetcode.cn/contest/autox2023/problems/BjAFy9/

题意

二分 + 动态规划

思路

  1. 非常不错的动态规划，设 $dp[i]$ 表示到达第 $days[i]$ 天前的最小开销，首先按照要求肯定对 $days$ 按照从小到大进行排序。此时我们肯定知道在 $days[0]$ 前的开销为 $0$，$dp[0] = 0$。我们初始化所有的 $dp[i]$ 为 $-1$。
  • 当我们在 $days[i]$ 处买票 $j$ 时，此时我们知道此时该套票可持续的时间为 $[days[i], days[i] + t[j] - 1]$，则下一次最优购票时间点应该是在大于等于 $days[i] + t[j]$ 且最接近 $days[i] + t[j]$ 的某一天 $days[k]$，我们可以用二分查找找到 $days[k]$。因此我们可以知道递推公式:
    $$
    dp[k] = min(dp[k], dp[i] + price[j])
    $$
  • 我们不需要每次都判断 $days[i]$，我们初始化 $dp[i] = \infty$ 进行标记，如上面所示一旦我们在 $days[i]$ 处选择了购置票 $j$ 时，最优选择肯定是从 $days[k]$ 处再购置新票，我们分别对最优选择点处进行标记，
  • 发现 $dp[i] = \infty$ 则跳过，因此此时该出购票肯定不是最优选择；
  • 发现 $dp[i] \neq \infty$ 时，我们选择购置新票，因此次时之前购置的票时间已经到期，需在此处重新购置新票；
  • 最后返回完成所有行程的最小值即可；
  1. 复杂度分析
  • 时间复杂度：时间复杂度为 $O(n \times m \times \log n)$，$n$ 为数组 $days$ 的长度，$m$ 为套票的种类数目。
  • 空间复杂度：空间复杂度为 $O(n)$，$n$ 为数组 $days$ 的长度。

代码

class Solution {
public:
    long long minCostToTravelOnDays(vector<int>& days, vector<vector<int>>& tickets) {
        int n = days.size();
        int m = tickets.size();
        sort(days.begin(), days.end());
        vector<long long> dp(n + 1, LONG_MAX);
        dp[0] = 0;
        for (int i = 0; i < n; i++) {
            if (dp[i] != LONG_MAX) {
                for (int j = 0; j < m; j++) {
                    int x = lower_bound(days.begin(), days.end(), days[i] + tickets[j][0]) - days.begin();
                    dp[x] = min(dp[x], dp[i] + tickets[j][1]);
                }
            }
        }
        return dp[n];
    }
};

AutoX-4. 蚂蚁爬行

题目

在一张稿纸上画了若干由线条构成的的线段和正圆形。geometry[i] 表示对于第 i 个线条有：

  • 若 geometry[i].length 为 4 ，表示为一条线段，[x1, y1, x2, y2] 表示该线段的两个端点坐标分别为 (x1,y1) 和 (x2,y2)。
  • 若 geometry[i].length 为 3 ，表示为一个正圆形，[x, y, r] 表示其圆心坐标和半径分别为 (x,y) 和 r

现有一群小蚂蚁在这些线条上爬行，path[i] = [start, end] 表示第 i 只蚂蚁从第 start 个线条前往第 end 个线条。在爬行过程中，对于任意两个线条，只要有接触（公共点），小蚂蚁就能从一个爬到另一个。请判断这些小蚂蚁能否到达各自的目的地。
示例 1：

输入：
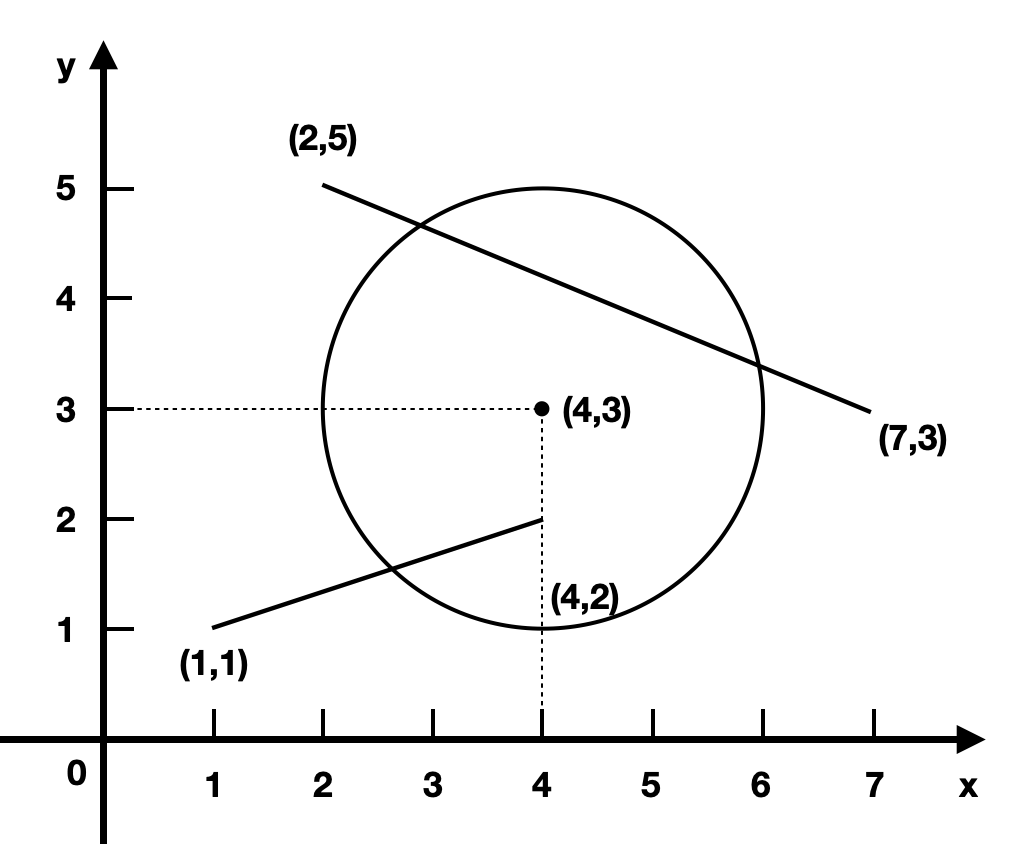
geometry = [[2,5,7,3],[1,1,4,2],[4,3,2]]
path = [[0,1],[1,2],[0,2]]

输出：[true,true,true]

解释：如下图所示：
所有的几何对象都是可互通的，所有蚂蚁都可以到达目的地。
image.png

示例 2：

输入：
geometry = [[4,1,1],[3,2,1],[1,4,5,4]]
path = [[0,1],[2,0]]

输出：[true,false]

解释：如下图所示:
geometry[0] 和 geometry[1] 相接触，geometry[2] 不与任何几何对象接触，因此蚂蚁 1 无法到达，
image.png

提示：

  • 2 <= geometry.length <= 1000
  • 0 <= geometry[i][0],geometry[i][1] <= 10^5
  • 对于线段，0 <= geometry[i][2],geometry[i][3] <= 10^5
  • 对于正圆形，1 <= geometry[i][2] <= 10^5
  • 1 <= path.length <= 1000
  • 0 <= path[i][0], path[i][1] < geometry.length

`

地址

https://leetcode.cn/contest/autox2023/problems/TcdlJS/

题意

几何 + 并查集

思路

  1. 从题目分析来看，本身题目思路非常简单，并查集的思想，但是写对不容易，涉及到计算几何的知识，真不是那么短时间内完全写正确。涉及以下检测：
  • 两个园是否存在交点；
  • 两个线段是否存在交点；
  • 线段和园是否存在交点；
    以上检测都不是那么容易短时间完全写对，下面的代码抄模板弄出来的。只需要依次检测第 $i$ 个图形是否与第 $j$ 个图形存在交点，如果存在交点则将两个图形所在的集合进行合并，所谓检测是否存在通路，即代表两个图形在一个集合中。
  1. 复杂度分析：
  • 时间复杂度：$O(n^2 \times \alpha(n) + m \times \alpha(n))$，其中 $n$ 表示数组的长度。
  • 空间复杂度：$(n)$，其中 $n$ 表示数组的长度。

代码

namespace xxx
{
    using Point = std::pair<double, double>;
    constexpr auto eps = 1e-12;

    double sq(double x) {
        return x * x;
    }

    std::vector<Point> intersects(const Point& p1, const Point& p2, const Point& cp, double r, bool segment) {
        std::vector<Point> res;
        auto x0 = cp.first;
        auto y0 = cp.second;
        auto x1 = p1.first;
        auto y1 = p1.second;
        auto x2 = p2.first;
        auto y2 = p2.second;
        auto A = y2 - y1;
        auto B = x1 - x2;
        auto C = x2 * y1 - x1 * y2;
        auto a = sq(A) + sq(B);
        double b, c;
        bool bnz = true;
        if (abs(B) >= eps) {
            b = 2 * (A * C + A * B * y0 - sq(B) * x0);
            c = sq(C) + 2 * B * C * y0 - sq(B) * (sq(r) - sq(x0) - sq(y0));
        }
        else {
            b = 2 * (B * C + A * B * x0 - sq(A) * y0);
            c = sq(C) + 2 * A * C * x0 - sq(A) * (sq(r) - sq(x0) - sq(y0));
            bnz = false;
        }
        auto d = sq(b) - 4 * a * c; // discriminant
        if (d < 0) {
            return res;
        }

        // checks whether a point is within a segment
        auto within = [x1, y1, x2, y2](double x, double y) {
            auto d1 = sqrt(sq(x2 - x1) + sq(y2 - y1));  // distance between end-points
            auto d2 = sqrt(sq(x - x1) + sq(y - y1));    // distance from point to one end
            auto d3 = sqrt(sq(x2 - x) + sq(y2 - y));    // distance from point to other end
            auto delta = d1 - d2 - d3;
            return abs(delta) < eps;                    // true if delta is less than a small tolerance
        };

        auto fx = [A, B, C](double x) {
            return -(A * x + C) / B;
        };

        auto fy = [A, B, C](double y) {
            return -(B * y + C) / A;
        };

        auto rxy = [segment, &res, within](double x, double y) {
            if (!segment || within(x, y)) {
                res.push_back(std::make_pair(x, y));
            }
        };

        double x, y;
        if (d == 0.0) {
            // line is tangent to circle, so just one intersect at most
            if (bnz) {
                x = -b / (2 * a);
                y = fx(x);
                rxy(x, y);
            }
            else {
                y = -b / (2 * a);
                x = fy(y);
                rxy(x, y);
            }
        }
        else {
            // two intersects at most
            d = sqrt(d);
            if (bnz) {
                x = (-b + d) / (2 * a);
                y = fx(x);
                rxy(x, y);
                x = (-b - d) / (2 * a);
                y = fx(x);
                rxy(x, y);
            }
            else {
                y = (-b + d) / (2 * a);
                x = fy(y);
                rxy(x, y);
                y = (-b - d) / (2 * a);
                x = fy(y);
                rxy(x, y);
            }
        }

        return res;
    }
}

namespace yyy
{
    using ll = long long;
    struct Point
    {
        ll x;
        ll y;
    };

    // Given three collinear points p, q, r, the function checks if
    // point q lies on line segment 'pr'
    bool onSegment(Point p, Point q, Point r)
    {
        if (q.x <= max(p.x, r.x) && q.x >= min(p.x, r.x) &&
            q.y <= max(p.y, r.y) && q.y >= min(p.y, r.y))
            return true;

        return false;
    }

    // To find orientation of ordered triplet (p, q, r).
    // The function returns following values
    // 0 --> p, q and r are collinear
    // 1 --> Clockwise
    // 2 --> Counterclockwise
    int orientation(Point p, Point q, Point r)
    {
        // See https://www.geeksforgeeks.org/orientation-3-ordered-points/
        // for details of below formula.
        ll val = (q.y - p.y) * (r.x - q.x) -
            (q.x - p.x) * (r.y - q.y);

        if (val == 0) return 0;  // collinear

        return (val > 0) ? 1 : 2; // clock or counterclock wise
    }

    // The main function that returns true if line segment 'p1q1'
    // and 'p2q2' intersect.
    bool doIntersect(Point p1, Point q1, Point p2, Point q2)
    {
        // Find the four orientations needed for general and
        // special cases
        ll o1 = orientation(p1, q1, p2);
        ll o2 = orientation(p1, q1, q2);
        ll o3 = orientation(p2, q2, p1);
        ll o4 = orientation(p2, q2, q1);

        // General case
        if (o1 != o2 && o3 != o4)
            return true;

        // Special Cases
        // p1, q1 and p2 are collinear and p2 lies on segment p1q1
        if (o1 == 0 && onSegment(p1, p2, q1)) return true;

        // p1, q1 and q2 are collinear and q2 lies on segment p1q1
        if (o2 == 0 && onSegment(p1, q2, q1)) return true;

        // p2, q2 and p1 are collinear and p1 lies on segment p2q2
        if (o3 == 0 && onSegment(p2, p1, q2)) return true;

        // p2, q2 and q1 are collinear and q1 lies on segment p2q2
        if (o4 == 0 && onSegment(p2, q1, q2)) return true;

        return false; // Doesn't fall in any of the above cases
    }
}

namespace zzz
{

    using Point = std::pair<double, double>;
    constexpr auto eps = 1e-12;

    double sq(double x) {
        return x * x;
    }

	bool doIntersect(Point p1, double r1, Point p2, double r2) {
		double dx = sq(p1.first - p2.first);
		double dy = sq(p1.second - p2.second);
		double dr = sq(r1 + r2);
        double dl = sq(r1 - r2);
		if (dx + dy <= dr && dx + dy >= dl) {
			return true;
		} else {
			return false;
		}
	}
}

class Solution {
public:
    bool isIntersect(vector<int>& a, vector<int>& b) {
        if (a.size() < b.size()) {
            return isIntersect(b, a);
        }
        if (a.size() == b.size() && a.size() == 3) {
            return zzz::doIntersect(zzz::Point(a[0], a[1]), a[2], zzz::Point(b[0], b[1]), b[2]);
        } else if (a.size() == b.size() && a.size() == 4) {
            return yyy::doIntersect(yyy::Point{a[0], a[1]}, yyy::Point{a[2], a[3]}, yyy::Point{b[0], b[1]}, yyy::Point{b[2], b[3]});
        } else if (a.size() == 4 &&b.size() == 3) {
            auto res = xxx::intersects(xxx::Point(a[0], a[1]), xxx::Point(a[2], a[3]), xxx::Point(b[0], b[1]), b[2], true);
            if (res.size() == 0) {
                return false;
            } else {
                return true;
            }
        }
        return true;
    }
    
    int find(vector<int> &f, int x) {
        while (x != f[x]) {
            x = f[x];
        }
        return x;
    }
    
    bool uni(vector<int> &f, int x, int y) {
        int fx = find(f, x);
        int fy = find(f, y);
        f[fx] = fy;
        return true;
    }
    
    vector<bool> antPass(vector<vector<int>>& geometry, vector<vector<int>>& path) {
        int m = geometry.size();
        int n = path.size();
        vector<int> f(m, 1);
        for (int i = 0; i < m; i++) {
            f[i] = i;
        }
        for (int i = 0; i < m; i++) {
            for (int j = i + 1; j < m; j++) {
                if (isIntersect(geometry[i], geometry[j])) {
                    uni(f, i, j);
                }
            }
        }
        vector<bool> ans;
        for (auto &v : path) {
            if (find(f, v[0]) == find(f, v[1])) {
                ans.emplace_back(true);
            } else {
                ans.emplace_back(false);
            }
        }
        return ans;
    }
};

欢迎关注和打赏，感谢支持！

Tags: 力扣周赛
← leetcode biweekly contest 86 leetcode weekly contest 308 →

扫描二维码，分享此文章