且听疯吟

leetcode weekly contest 307

2022-11-01

leetcode weekly contest 307

周赛题目质量确实挺高的，最后一题还是不会。

2383. 赢得比赛需要的最少训练时长

题目

校运动会上，所有参赛同学身上都贴有他的参赛号码。某班参赛同学的号码记于数组 nums 中。假定反转后的号码称为原数字的「镜像号码」。如果 两位同学 满足条件：镜像号码 A + 原号码 B = 镜像号码 B + 原号码 A，则这两位同学可以到广播站兑换一次读通讯稿的机会，为同班同学加油助威。请返回所有参赛同学可以组成的可以读通讯稿的组数，并将结果对10^9+7取余。

注意：

  1. 镜像号码中如存在前置零，则忽略前置零。
  2. 同一位同学可有多次兑换机会。

示例 1：

输入：nums = [17,28,39,71]

输出：3

解释：
共有三对同学，分别为 [17,28]、[17,39]、[28,39]。其中：
第一对同学：17 + 82 = 71 + 28；
第二对同学：17 + 93 = 71 + 39；
第三对同学：28 + 93 = 82 + 39。

示例 2：

输入：nums = [71, 60]

输出：1

解释：
共有一对同学，为 [71, 60]。
因为 71 + 6 = 17 + 60，此处 60 的镜像号码为 6，前导零被忽略。

提示：

  • 0 <= nums.length <= 10^6
  • 0 <= nums[i] <= 10^9

地址

https://leetcode.cn/problems/minimum-hours-of-training-to-win-a-competition/

题意

贪心算法

思路

  1. 简单的贪心算法，每次遇到不足时，则进行增加刚好比当前的元素的能量和经验大 $1$ 即可。
  2. 复杂度分析：
  • 时间复杂度：$O(n)$，其中 $n$ 表示数组的长度。
  • 空间复杂度：$O(1)$。

代码

class Solution {
public:
    int minNumberOfHours(int initialEnergy, int initialExperience, vector<int>& energy, vector<int>& experience) {
        int tot = 0;
        int n = energy.size();
        for (int i = 0; i < n; i++) {
            if (energy[i] >= initialEnergy) {
                int add = energy[i] - initialEnergy + 1;
                initialEnergy += add;
                tot += add;
            }
            if (experience[i] >= initialExperience) {
                int add = experience[i] - initialExperience + 1;
                initialExperience += add;
                tot += add;
            }
            initialEnergy -= energy[i];
            initialExperience += experience[i];
        }
        
        return tot;
    }
};

2384. 最大回文数字

题目

给你一个仅由数字（0 - 9）组成的字符串 num 。

请你找出能够使用 num 中数字形成的 最大回文 整数，并以字符串形式返回。该整数不含 前导零 。

注意：

  • 你 无需 使用 num 中的所有数字，但你必须使用 至少 一个数字。
  • 数字可以重新排序。

示例 1：

输入：num = "444947137"
输出："7449447"
解释：
从 "444947137" 中选用数字 "4449477"，可以形成回文整数 "7449447" 。
可以证明 "7449447" 是能够形成的最大回文整数。

示例 2：

输入：num = "00009"
输出："9"
解释：
可以证明 "9" 能够形成的最大回文整数。
注意返回的整数不应含前导零。

提示：

  • 1 <= num.length <= 105
  • num 由数字（0 - 9）组成

地址

https://leetcode.cn/contest/weekly-contest-307/problems/largest-palindromic-number/

题意

贪心法

思路

  1. 简单的贪心法即可，回文数分为左右两部分，我们贪心的选择左边的最大部分即可，按照最大的数字尽可能的往左半边放置的原则，优先从 $9$ 开始进行选择直到 $1$ 为止。右边的回文部分则是左边的镜像。此时需要注意的时我们还需要选择回文数的中间那个数字也是按照贪心的原则去选择即可。
  2. 复杂度分析：
  • 时间复杂度：时间复杂度为 $O(n + |\Sigma|)$，$n$ 表示字符串的长度，$|\Sigma|$ 表示字符集。
  • 空间复杂度：时间复杂度为 $O(n)$，$n$ 表示字符串的长度。

代码

class Solution {
public:
    string largestPalindromic(string num) {
        vector<int> cnt(10);
        string ans;
        for(auto c : num) {
            cnt[c - '0']++;
        }
        string prefix;
        for(int i = 9; i >= 0; i--) {
            if(cnt[i] > 0) {
                int tot = cnt[i] / 2;
                for(int j = 0; j < tot; j++) {
                    prefix.push_back(i + '0');
                }
                cnt[i] = cnt[i] % 2;
            }
        }
        
        string suffix = prefix;
        reverse(suffix.begin(), suffix.end());
        for(int i = 9; i >= 0; i--) {
            if(cnt[i] > 0) {
                char c = i + '0';
                if(prefix.size() > 0 && prefix[0] != '0') {
                    return prefix + string(1, c) + suffix;
                } else {
                    return string(1, c);
                }
            }
        }
        if (prefix.size() > 0 && prefix[0] != '0') {
            return prefix + suffix;
        } else {
            return "0";
        }
    }
};

2385. 感染二叉树需要的总时间

题目

给你一棵二叉树的根节点 root ，二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟，感染 将会从值为 start 的节点开始爆发。

每分钟，如果节点满足以下全部条件，就会被感染：

  • 节点此前还没有感染。
  • 节点与一个已感染节点相邻。

返回感染整棵树需要的分钟数。

示例 1：

img

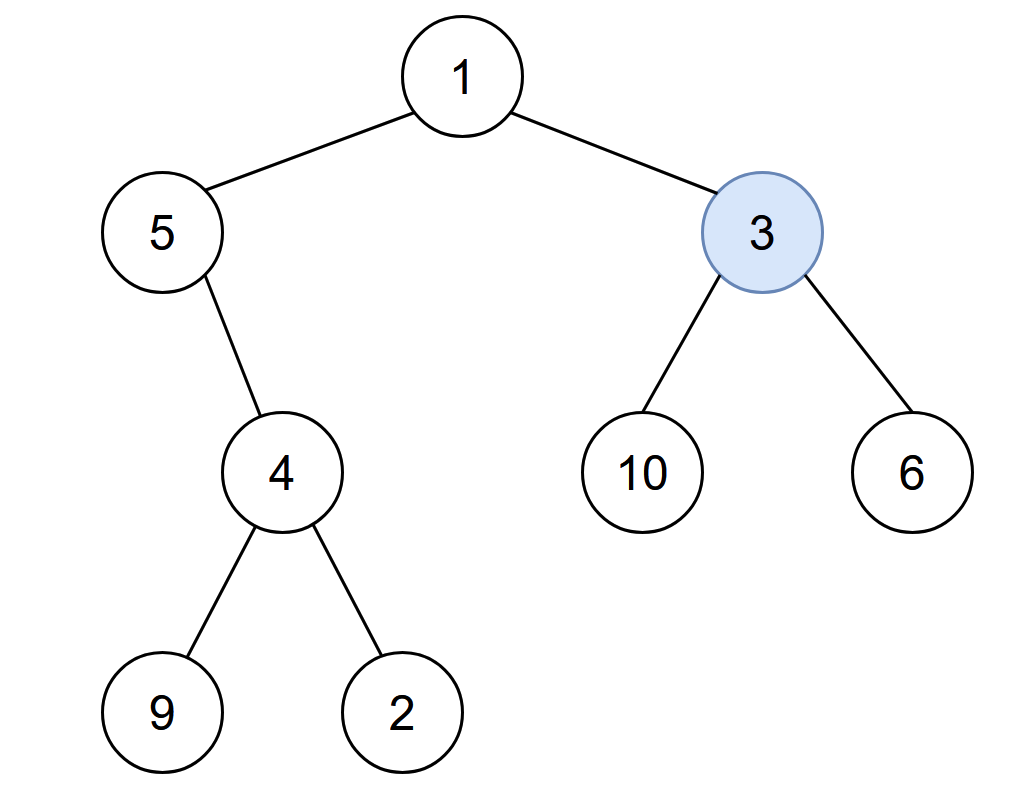
输入：root = [1,5,3,null,4,10,6,9,2], start = 3
输出：4
解释：节点按以下过程被感染：
- 第 0 分钟：节点 3
- 第 1 分钟：节点 1、10、6
- 第 2 分钟：节点5
- 第 3 分钟：节点 4
- 第 4 分钟：节点 9 和 2
感染整棵树需要 4 分钟，所以返回 4 。

示例 2：

img

输入：root = [1], start = 1
输出：0
解释：第 0 分钟，树中唯一一个节点处于感染状态，返回 0 。

提示：

  • 树中节点的数目在范围 [1, 105] 内
  • 1 <= Node.val <= 105
  • 每个节点的值 互不相同
  • 树中必定存在值为 start 的节点

地址

https://leetcode.cn/problems/amount-of-time-for-binary-tree-to-be-infected/

题意

BFS

思路

  1. 题目本身比较简单了，最大的问题是我们无法从孩子节点访问父节点，此时我们只需要重新建树，使得孩子节点可以访问父亲节点即可，那么就转换为普通题目了，按照标准的 $BFS$ 模板遍历即可。
  • 时间复杂度：时间复杂度为 $O(n)$，$n$ 为节点数目。
  • 空间复杂度：空间复杂度为 $O(n)$，$n$ 为节点数目。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

struct MyTreeNode {
    int val;
    MyTreeNode *left;
    MyTreeNode *right;
    MyTreeNode *parent;
    MyTreeNode() : val(0), left(nullptr), right(nullptr), parent(nullptr) {}
    MyTreeNode(int x) : val(x), left(nullptr), right(nullptr), parent(nullptr) {}
    MyTreeNode(int x, MyTreeNode *left, MyTreeNode *right, MyTreeNode *parent) : val(x), left(left), right(right),parent(parent) {}
};

class Solution {
public:
    int amountOfTime(TreeNode* root, int start) {
        MyTreeNode *myRoot = new MyTreeNode();
        MyTreeNode *target = nullptr;
        queue<pair<TreeNode *, MyTreeNode *>> qu;
        qu.emplace(root, myRoot);
        while(!qu.empty()) {
            auto [node, myNode] = qu.front();
            qu.pop();
            myNode->val = node->val;
            if(myNode->val == start) {
                target = myNode;
            }
            if(node->left) {
                myNode->left = new MyTreeNode();
                myNode->left->val = node->left->val;
                myNode->left->parent = myNode;
                qu.emplace(node->left, myNode->left);
            }
            if(node->right) {
                myNode->right = new MyTreeNode();
                myNode->right->val = node->right->val;
                myNode->right->parent = myNode;
                qu.emplace(node->right, myNode->right);
            }
        }
        
        queue<MyTreeNode *> Q;
        unordered_set<int> visit;
        Q.emplace(target);
        visit.emplace(target->val);
        int ans = -1;
        while(!Q.empty()) {
            int sz = Q.size();
            for (int i = 0; i < sz; i++) {
                auto curr = Q.front();
                Q.pop();
                if (curr->left && !visit.count(curr->left->val)) {
                    visit.emplace(curr->left->val);
                    Q.emplace(curr->left);
                }
                if (curr->right && !visit.count(curr->right->val)) {
                    visit.emplace(curr->right->val);
                    Q.emplace(curr->right);
                }
                if (curr->parent && !visit.count(curr->parent->val)) {
                    visit.emplace(curr->parent->val);
                    Q.emplace(curr->parent);
                }
            }
            ans++;
        }
        return ans;
    }
};

2386. 找出数组的第 K 大和

题目

给你一个整数数组 nums 和一个 正 整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。

数组的 第 k 大和 定义为：可以获得的第 k 个 最大 子序列和（子序列和允许出现重复）

返回数组的 第 k 大和 。

子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。

注意：空子序列的和视作 0 。

示例 1：

输入：nums = [2,4,-2], k = 5
输出：2
解释：所有可能获得的子序列和列出如下，按递减顺序排列：
- 6、4、4、2、2、0、0、-2
数组的第 5 大和是 2 。

示例 2：

输入：nums = [1,-2,3,4,-10,12], k = 16
输出：10
解释：数组的第 16 大和是 10 。

提示：

  • n == nums.length
  • 1 <= n <= 105
  • -109 <= nums[i] <= 109
  • 1 <= k <= min(2000, 2n)

地址

https://leetcode.cn/contest/ubiquant2022/problems/I3Gm2h/

题意

堆

思路

  1. 这个题目确实比较难的题目，但是还是非常好且值得思考的题目。确实不是容易理解的一个题目。需要需要注意的是从数组 $[1,2,3,4,5]$ 中找到前 $k$ 项的子序列最小和来寻找思路：
  • 我们知道最小的序列肯定是 $[1]$, 此时 $[1]$ 之后我们的待选序列为$[1,2], [2]$，选择下一个元素后要么保留前一个元素，要么不保留前一个元素。这个是解题的关键思路。
  1. 复杂度分析：
  • 时间复杂度：$O(n \times \log n + k \times \log k)$，其中 $n$ 表示数组的长度。
  • 空间复杂度：$O(k)$。

代码

  • 堆
    class Solution {
    public:
        long long kSum(vector<int>& nums, int k) {
            long long sum = 0;
            for (auto &num : nums) {
                if (num >= 0) {
                    sum += num;
                } else {
                    num = -num;
                }
            }
            priority_queue<pair<long long, int>> pq;
            sort(nums.begin(), nums.end());
            pq.emplace(sum, 0);
            long long ans = 0;
            while(k > 0) {
                auto [curr, len] = pq.top();
                pq.pop();
                ans = curr;
                if (len < nums.size()) {
                    pq.emplace(curr - nums[len], len + 1);
                    if (len > 0) {
                        pq.emplace(curr - nums[len] + nums[len - 1], len + 1);
                    }
                }
                k--;
            }
            return ans;        
        }
    };

欢迎关注和打赏，感谢支持！

Tags: 力扣周赛
← leetcode weekly contest 308 九坤投资专场竞赛 →

扫描二维码，分享此文章