九坤投资专场竞赛
比赛的题目质量还是挺高的,第四题还是蛮有意思的题目,前三题都水题了。
九坤-01. 可以读通讯稿的组数
题目
校运动会上,所有参赛同学身上都贴有他的参赛号码。某班参赛同学的号码记于数组 nums 中。假定反转后的号码称为原数字的「镜像号码」。如果 两位同学 满足条件:镜像号码 A + 原号码 B = 镜像号码 B + 原号码 A,则这两位同学可以到广播站兑换一次读通讯稿的机会,为同班同学加油助威。请返回所有参赛同学可以组成的可以读通讯稿的组数,并将结果对10^9+7取余。
注意:
- 镜像号码中如存在前置零,则忽略前置零。
- 同一位同学可有多次兑换机会。
示例 1:
输入:
nums = [17,28,39,71]输出:
3解释:
共有三对同学,分别为 [17,28]、[17,39]、[28,39]。其中:
第一对同学:17 + 82 = 71 + 28;
第二对同学:17 + 93 = 71 + 39;
第三对同学:28 + 93 = 82 + 39。
示例 2:
输入:
nums = [71, 60]输出:
1解释:
共有一对同学,为 [71, 60]。
因为 71 + 6 = 17 + 60,此处 60 的镜像号码为 6,前导零被忽略。
提示:
0 <= nums.length <= 10^60 <= nums[i] <= 10^9
地址
https://leetcode.cn/contest/ubiquant2022/problems/xdxykd/
题意
哈希统计
思路
- 常规题目了,等式变换即可,镜像号码 A + 原号码 B = 镜像号码 B + 原号码 A 变换为: 镜像号码 A - 原号码 A = 镜像号码 B - 原号码 B。我们只需要统计 $x$ 减去镜像 $x$ 的数目 $y$ 即可,此时构成的相等的个数为 $\dfrac{y \times (y - 1)}{2}$,我们依次统计所有的数目之和即可。
- 复杂度分析:
- 时间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
- 空间复杂度:$O(n)$,其中 $n$ 表示数组的长度。
代码
class Solution { |
九坤-02. 池塘计数
题目
最近的降雨,使田地中的一些地方出现了积水,field[i][j] 表示田地第 i 行 j 列的位置有:
- 若为
W, 表示该位置为积水; - 若为
., 表示该位置为旱地。
已知一些相邻的积水形成了若干个池塘,若以 W 为中心的八个方向相邻积水视为同一片池塘。
请返回田地中池塘的数量。
示例 1:
输入:
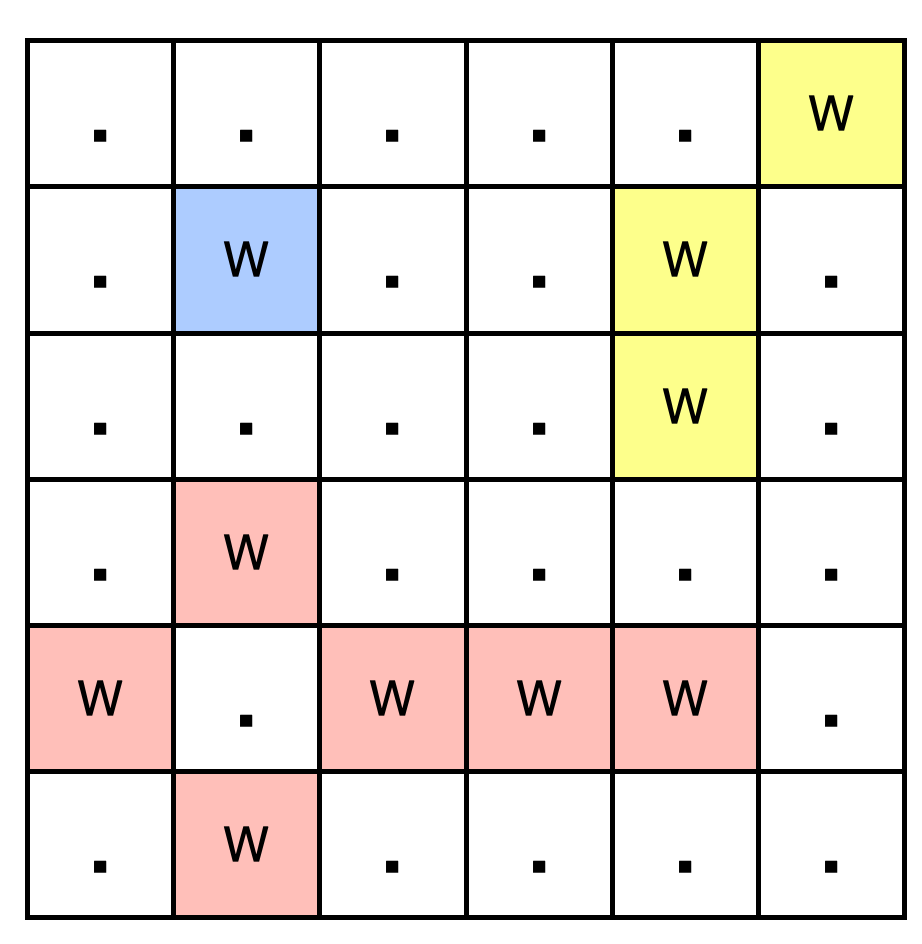
field = [".....W",".W..W.","....W.",".W....","W.WWW.",".W...."]输出:
3解释:如下图所示,共有 3 个池塘:
示例 2:
输入:
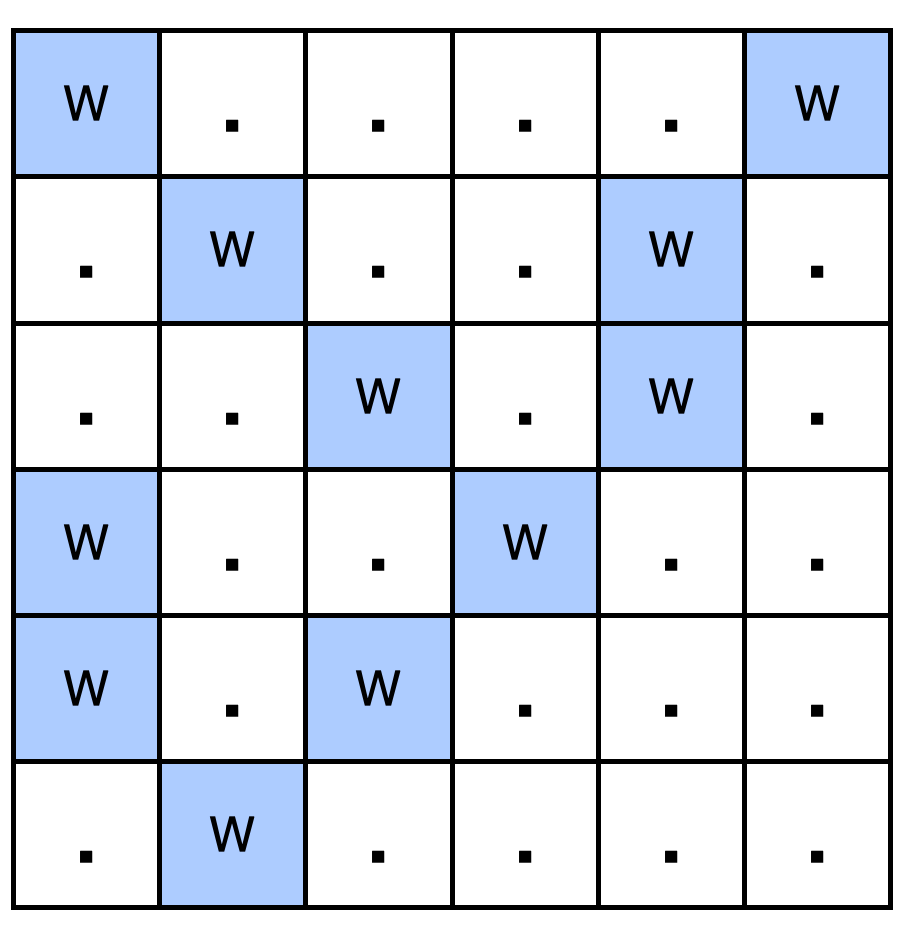
field = ["W....W",".W..W.","..W.W.","W..W..","W.W...",".W...."]输出:
1解释:如下图所示,共有 1 个池塘:
提示:
1 <= field.length, field[i].length <= 100field中仅包含W和.
地址
https://leetcode.cn/contest/ubiquant2022/problems/3PHTGp/
题意
BFS 或者 并查集
思路
- 没啥好说的直接 $8$ 个方向的 $BFS$ 遍历即可,非常简单的模板题。另一种解法为并查集,感觉也是模板,没啥好说的。
- 复杂度分析:
- 时间复杂度:时间复杂度为 $O(n \times m)$,$n, m$ 表示矩阵的行与列。
- 空间复杂度:时间复杂度为 $O(n \times m)$,$n, m$ 表示矩阵的行与列。
代码
BFS
class Solution { |
6158. 九坤-03. 数字默契考验
题目
某数学兴趣小组有 N 位同学,编号为 0 ~ N-1,老师提议举行一个数字默契小测试:首先每位同学想出一个数字,按同学编号存于数组 numbers。每位同学可以选择将自己的数字进行放大操作,每次在以下操作中任选一种(放大操作不限次数,可以不操作):
- 将自己的数字乘以 2
- 将自己的数字乘以 3
若最终所有同学可以通过操作得到相等数字,则返回所有同学的最少操作次数总数;否则请返回 -1。
示例 1:
输入:numbers = [50, 75, 100] |
示例 2:
输入:numbers = [10, 14] |
提示:
1 <= numbers.length <= 10^51 <= numbers[i] <= 10^9
地址
https://leetcode.cn/contest/ubiquant2022/problems/uGuf0v/
题意
数学问题
思路
- 本质是我们求出 $numbers$ 数组中所有元素的最小公倍数 $x$,然后分别检测数组的每个元素 $\dfrac{x}{numbers[i]}$ 是否只包含因子 $2$ 与因子 $3$,当然求最小公倍数会溢出,所以这个方法需要稍微一点技巧,就时首先将所有元素去掉其中最大公约数。
- 数组 $nums$ 的所有元素 $nums[i]$ 去掉质因子 $2,3$ 以后的值为 $p[i]$,此时所有元素含有的 $p[i]$ 含有的质因子一定相同,否则两个元素不可能通过乘以 $2,3$ 变为相同元素,这个可以很容易证明。假设 $x = \prod_{i=1}^{n}\limits p_i^{c_i}, y = \prod_{i=1}^{m}\limits p_i^{c_i}$,如果 $x$ 与 $y$ 可以通过乘以 $2,3$ 变为相同的数,则两个数一定含有相同的质因子。此时我们只需要求出所有元素含有的因子 $2,3$ 的最大数目 $cnt_1, cnt_2$,则最终的数含有的 $2,3$ 因子的最大数目为 $cnt_1, cnt_2$。
- 时间复杂度:时间复杂度为 $O(n \log n)$,$n$ 为数组的长度。
- 空间复杂度:空间复杂度为 $O(n)$,其中 $n$ 为数组的长度。
代码
class Solution { |
- 数学
class Solution {
public:
int minOperations(vector<int>& nums) {
int n = nums.size();
vector<int> cnt1(n), cnt2(n);
for (int i = 0; i < n; i++) {
while(nums[i] % 2 == 0) {
nums[i] /= 2;
cnt1[i]++;
}
while(nums[i] %3 == 0) {
nums[i] /= 3;
cnt2[i]++;
}
if (i > 0 && nums[i] != nums[i - 1]) {
return -1;
}
}
int ans = 0;
int maxCnt1 = *max_element(cnt1.begin(), cnt1.end());
int maxCnt2 = *max_element(cnt2.begin(), cnt2.end());
for (int i = 0; i < n; i++) {
ans += maxCnt1 - cnt1[i];
ans += maxCnt2 - cnt2[i];
}
return ans;
}
};
九坤-04. 筹码游戏
题目
九坤很喜欢玩德州扑克,但是有一个神奇的周五,大家都去加班了,于是九坤只能研究起了桌上的筹码。
他把所有的筹码都放入了一个纸箱中,并按以下规则向外抽取筹码:
每次抽取仅取出
1个筹码如果对本次取出的筹码不满意,会将该筹码放回并重新抽取,直到确定想要这个筹码。
对于取出的筹码,他会将相同面值的筹码放在一堆
例如:抽取了
6个筹码,3个10,2个5,1个1,那么他就会把这些筹码放成三堆,数量分别是3、2、1。
纸箱中共有 kind 种面值的筹码。现给定九坤取出筹码的最终目标为 nums, nums[i] 表示第 i 堆筹码的数量。
假设每种面值的筹码都有无限多个,且九坤总是遵循最优策略,使得他达成目标的操作次数最小化。
请返回九坤达成目标的情况下,需要取出筹码次数的期望值。
注意:
- 最终取出的筹码中,对于任意两堆筹码的面值都是不同的。
- 不需要考虑筹码堆的顺序(例如,[3,1,1]、[1,1,3] 这两个筹码堆是相同的)
示例 1:
输入:
nums = [1,1]kind = 2
输出:3.00000解释:共有 2 种筹码,初始取出的数量为
[0,0]
第一次取出筹码后,筹码数量为[1,0],此时取了1次
第二次取出筹码后,筹码数量为[2,0]和[1,1]的概率均为0.5
因此,在 [1,0] 的基础上取出[1,1]的次数期望值为2
总期望值为1+2=3
示例 2:
输入:
nums = [1,2]kind = 4
输出:3.833333解释:
1 + 1 + 1/4 * 4/3 + 3/4 * 4/2 = 23 / 6
提示:
1 <= kind <= 501 <= nums.length <= kindsum(nums[0],nums[1],...,nums[n]) <= 50
地址
https://leetcode.cn/contest/ubiquant2022/problems/I3Gm2h/
题意
数论与概率
思路
- 该题目重点是对求期望的理解。定义状态为一个数组 $[c_0, c_1, c_2, c_3, \cdots, c_m-1]$,$c_i$ 表示当前已抽取的不同种类的筹码的数量,设最终状态为 $nums$,且按照从小到大进行排序。设从状态 $s_0$ 到 最终状态的期望为 $E_{s_0}$,而 $s_0$ 在经过一次抽取后有以下两种情况:
- 合法的状态:设合法的状态为 $s_1, s_2, s_3, \cdots,s_{t-1}$,且每个状态中的数量都是按照从小到大进行排列,此时合法状态 $i$ 中每个元素 $c_{ij}$ 一定满足 $c_{ij} \le nums_{j}$,否则就不能称为合法状态。设从状态 $s_0$ 变为合法状态 $s_1, s_2, s_3, \cdots,s_{t}$ 的概率为 $p_1,p_2, \cdots, p_{t-1}$,设合法状态 $s_1, s_2, s_3, \cdots,s_{t}$ 的变为最终状态的期望为 $E_1,E_2, \cdots, E_{t}$。
- 非法状态:即此时非法状态 $s_1^{‘},s_2^{‘},s_3^{‘}, \cdots, s_k^{‘}$ 出现了 $c_{ij} \le nums_{j}$,按照题目要求如果出现了非法状态,我们应当将选择的筹码放回重新抽取,则状态 $s_i^{‘}$ 又回到了初始化状态 $s_0$。设从状态 $s_0$ 变为非法法状态 $s_1^{‘}, s_2^{‘}, s_3^{‘}, \cdots,s_{k}^{‘}$ 的概率为 $p_1^{‘},p_2^{‘}, \cdots, p_{k}^{‘}$,也即 $s_0$ 继续停留在状态 $s_0$ 的概率为 $\sum_{i=1}^{k} \limits p_i^{‘}$。
则此时我们可以知道状态 $s_0$ 的期望如下:
$$
E_{s_0} = \sum_{i=1}^{t}(E_{s_i} + 1) * p_i + \sum_{i=1}^{k}(E_{s_0} + 1) * p_i^{‘} \
$$
由于我们知道状态转换只有两种可能,要么为非法要么为合法状态,因此可以知道:$$\sum_{i=1}^{t} \limits p_i + \sum_{i=1}^{k} \limits p_i^{‘} = 1$$
所以上述等式可以变换为如下:
$$
E_{s_0} = \sum_{i=1}^{t} (E_{s_i} + 1) * p_i + (1 - \sum_{i=1}^{t}p_i) * (E_{s_0} + 1) \
= \sum_{i=1}^{t} E_{s_i} * p_i + (1 - \sum_{i=1}^{t}p_i) * E_{s_0} + 1\
= \frac{\sum_{i=1}^{t} \limits E_{s_i} * p_i + 1}{1 - \sum_{i=1}^{t} \limits p_i}
$$
2. 根据以上递推公式就非常好办了,初始时从状态 $s_0 = [0,0,0,\cdots, 0]$ 开始搜索,状态 $s_0$ 可以转换的合法状态为 $s_1 = [1,0,0,\cdots, 0],s_2 = [0,1,0,\cdots, 0],s_3 = [0,0,1,\cdots, 0],\cdots$,一共有 $kind$ 种状态,可以进行如下减枝技巧:
- 可以用哈希表存储每个状态,此时如果当前状态已经搜索过,则直接返回;
- 我们可以观察到,实际上从 $s_0$ 进行状态转移时,每种状态的概率均为 $\dfrac{1}{kind}$,所以此时就非常简单了,我们只需求出合法的状态数量即可。
- 合法状态实际上很多为同一种状态,可以进行合并,不需要每次都计算,$s_1 = [1,0,0,\cdots, 0],s_2 = [0,1,0,\cdots, 0],s_3 = [0,0,1,\cdots, 0],\cdots$ 这些状态均为同一种状态。我们按照从小到大进行排序,每次选择在相同的元素的末尾的一个元素进行加 $1$ 即可,即可减少状态计算。
- 复杂度分析:
- 时间复杂度:$O(kind \times sum(nums))$,其中 $sum(nums)$ 表示数组中所有元素的和,$kind$ 表示筹码的种类。
- 空间复杂度:$O(sum(nums))$,最终只含有 $sum(nums)$ 种状态。
代码
- 二分查找
class Solution {
public:
double chipGame(vector<int>& nums, int kind) {
int n = nums.size();
int total = accumulate(nums.begin(), nums.end(), 0);
nums.resize(kind);
vector<int> curr(kind);
sort(nums.begin(), nums.end());
map<vector<int>, double> memo;
function<double(vector<int>&, int)> dfs = [&](vector<int> &state, int m)->double {
if (m == 0) {
return 0.0;
}
if (memo.count(state)) {
return memo[state];
}
double ret = 0.0;
int cnt = 0;
for (int i = 0, j = 0; i < kind; i = j) {
j = i;
while (j < kind && state[j] == state[i]) {
j++;
}
state[j - 1]++;
if (state[j - 1] <= nums[j - 1]) {
ret += dfs(state, m - 1) * (j - i) / kind;
cnt += j - i;
}
state[j - 1]--;
}
ret = (ret + 1) * kind / cnt;
memo[state] = ret;
return ret;
};
return dfs(curr, total);
}
};
欢迎关注和打赏,感谢支持!
- 关注我的博客: http://mikemeng.org/
- 关注我的知乎:https://www.zhihu.com/people/da-hua-niu
- 关注我的微信公众号: 公务程序猿

扫描二维码,分享此文章